题目内容
13. 如图,BC是圆O的一条弦,延长BC至点E,使得BC=2CE=2,过E作圆O的切线,A为切点,∠BAC的平分线AD交BC于点D,则DE的长为$\sqrt{3}$.
如图,BC是圆O的一条弦,延长BC至点E,使得BC=2CE=2,过E作圆O的切线,A为切点,∠BAC的平分线AD交BC于点D,则DE的长为$\sqrt{3}$.
分析 利用切线的性质、角平分线的性质,证明∠ADE=∠DAE,可得AE=DE,再利用切割线定理,即可求出DE的长.
解答 解:∵AE是圆O的切线,
∴∠EAC=∠B,
又∵AD是∠BAC的平分线,∴∠BAD=∠DAC.
∴∠ADE=∠DAE,
∴AE=DE,
∵BC=2CE=2,AE是圆O的切线,
∴AE2=CE•BE=3,
∴AE=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查切线的性质、角平分线的性质,考查切割线定理,考查学生的计算能力,比较基础.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,M是棱PD的中点,且PA=AB=AC=2,BC=2$\sqrt{2}$.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,M是棱PD的中点,且PA=AB=AC=2,BC=2$\sqrt{2}$.  如图是某直三棱柱(侧棱与底面垂直的三棱柱)被削去上底后的直观图与三视图中的侧视图、俯视图,在直观图中,M是BD的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
如图是某直三棱柱(侧棱与底面垂直的三棱柱)被削去上底后的直观图与三视图中的侧视图、俯视图,在直观图中,M是BD的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示. 已知三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB=5,AC=4,BC=3,AA1=4,点D在AB上.
已知三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB=5,AC=4,BC=3,AA1=4,点D在AB上. 如图,△ABC中,∠ACB=90°,D是AC上一点,以AD为直径作⊙O交AB于点G
如图,△ABC中,∠ACB=90°,D是AC上一点,以AD为直径作⊙O交AB于点G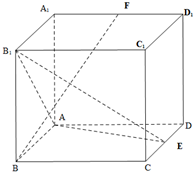 如图:在长方体ABCD-A1B1C1D1中,AB=2,BC=4,BB1=4,E是CD的中点,F是A1D1的中点.
如图:在长方体ABCD-A1B1C1D1中,AB=2,BC=4,BB1=4,E是CD的中点,F是A1D1的中点.