Question

14．正四面体S-ABC的所有棱长都为2，则它的体积为$\frac{2\sqrt{2}}{3}$．

Answer 1

分析 由正四面体的棱长为1，所以此四面体一定可以放在棱长为$\sqrt{2}$的正方体中，由此能求出此四面体的体积．

解答 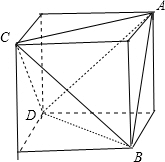解：∵正四面体的棱长为2，
∴此四面体一定可以放在正方体中，
∴我们可以在正方体中寻找此四面体．
如图所示，四面体ABCD满足题意，BC=2，
∴正方体的棱长为$\sqrt{2}$，
∴此四面体的体积为$（\sqrt{2}）^{3}$-$4×\frac{1}{3}×\frac{1}{2}×\sqrt{2}×\sqrt{2}×\sqrt{2}$=$\frac{2\sqrt{2}}{3}$．
故答案为：$\frac{2\sqrt{2}}{3}$．

点评 本题考查四面体的体积问题，考查了空间想象能力，其解答的关键是在正方体中寻找此四面体．