题目内容
14.已知定义y=log(x+1)F(x,y),若e<x<y,证明:F(x-1,y)>F(y-1,x)分析 通过对数与指数之间的关系可知问题转化为证明xy>yx,变形后即证$\frac{lnx}{x}$>$\frac{lny}{y}$,通过构造函数h(x)=$\frac{lnx}{x}$,利用导数知识可知函数h(x)在区间(e,+∞)上单调递减,进而可得结论.
解答 证明:∵y=log(x+1)F(x,y),
∴F(x,y)=(1+x)y,
∴F(x-1,y)=xy,F(y-1,x)=yx,
依题意,问题转化为证明xy>yx,
即证ylnx>xlny,即证$\frac{lnx}{x}$>$\frac{lny}{y}$,
记h(x)=$\frac{lnx}{x}$,则h′(x)=$\frac{1-lnx}{{x}^{2}}$,
∵当x>e时,h′(x)>0,
∴函数h(x)在区间(e,+∞)上单调递减,
又∵e<x<y,
∴h(x)>h(y),
即F(x-1,y)>F(y-1,x).
点评 本题考查不等式的证明,涉及函数单调性等基础知识,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
3.已知函数f(x)=|x|-1,若关于x的方程f2(x)+(2m-1)f(x)+4-2m=0有四个不同的实数解,则实数m的取值范围是( )
| A. | m<-2 | B. | m<-2.5 | C. | m<1.5 | D. | m>1.5 |
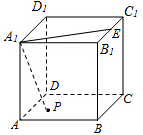 如图,正方体ABCD-A1B1C1D1中,E是棱B1C1的中点,动点P为正方体各面上的任一点.
如图,正方体ABCD-A1B1C1D1中,E是棱B1C1的中点,动点P为正方体各面上的任一点. 如图,平面AEFD⊥平面BCFE,其中AEFD为正方形,BCFE为直角梯形,BE∥CF,BE⊥EF,BE=EF=$\frac{1}{2}$CF=1.
如图,平面AEFD⊥平面BCFE,其中AEFD为正方形,BCFE为直角梯形,BE∥CF,BE⊥EF,BE=EF=$\frac{1}{2}$CF=1.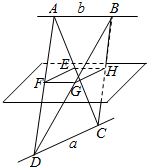 如图,平面EFGH分别平行于CD,AB,点E,F,G,H分别在AC,AD,BD,BC上,且CD=a,AB=b,CD⊥AB.
如图,平面EFGH分别平行于CD,AB,点E,F,G,H分别在AC,AD,BD,BC上,且CD=a,AB=b,CD⊥AB.