题目内容
已知抛物线y2=x和三个点M(x0,y0)、P(0,y0)、N(-x0,y0)(y0≠x02,y0>0),过点M的一条直线交抛物线于A、B两点,AP、BP的延长线分别交曲线C于E、F,
(1)证明E、F、N三点共线;
(2)如果A、B、M、N四点共线,问:是否存在y0,使以线段AB为直径的圆与抛物线有异于A、B的交点?如果存在,求出y0的取值范围,并求出该交点到直线AB的距离;若不存在,请说明理由.
(1)证明E、F、N三点共线;
(2)如果A、B、M、N四点共线,问:是否存在y0,使以线段AB为直径的圆与抛物线有异于A、B的交点?如果存在,求出y0的取值范围,并求出该交点到直线AB的距离;若不存在,请说明理由.
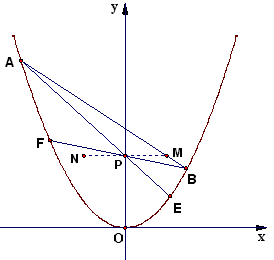
(1)证明:设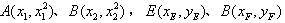 ,
,
则直线AB的方程: ,
,
即: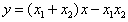 ,
,
因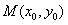 在AB上,所以
在AB上,所以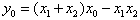 ,①
,①
又直线AP方程: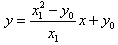 ,
,
由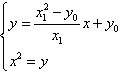 得:
得: ,
,
所以 ,
,
同理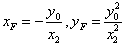 ,
,
所以直线EF的方程: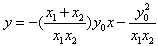 ,
,
令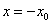 得
得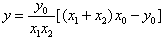 ,
,
将①代入上式得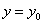 ,即N点在直线EF上,所以E,F,N三点共线;
,即N点在直线EF上,所以E,F,N三点共线;
(2)解:由已知A、B、M、N共线,所以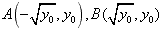 ,
,
以AB为直径的圆的方程: ,
,
由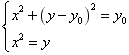 得
得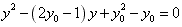 ,
,
所以 ,
,
要使圆与抛物线有异于A,B的交点,则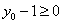 ,
,
所以存在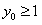 ,使以AB为直径的圆与抛物线有异于A,B的交点
,使以AB为直径的圆与抛物线有异于A,B的交点 ,
,
则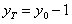 ,
,
所以交点T到AB的距离为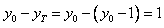 。
。
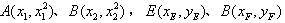 ,
,则直线AB的方程:
 ,
,即:
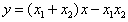 ,
,因
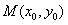 在AB上,所以
在AB上,所以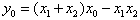 ,①
,① 又直线AP方程:
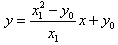 ,
,由
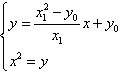 得:
得: ,
,所以
 ,
,同理
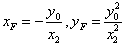 ,
,所以直线EF的方程:
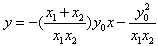 ,
,令
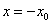 得
得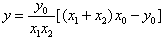 ,
,将①代入上式得
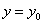 ,即N点在直线EF上,所以E,F,N三点共线;
,即N点在直线EF上,所以E,F,N三点共线;(2)解:由已知A、B、M、N共线,所以
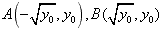 ,
,以AB为直径的圆的方程:
 ,
,由
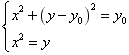 得
得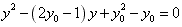 ,
,所以
 ,
,要使圆与抛物线有异于A,B的交点,则
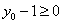 ,
,所以存在
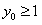 ,使以AB为直径的圆与抛物线有异于A,B的交点
,使以AB为直径的圆与抛物线有异于A,B的交点 ,
,则
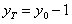 ,
,所以交点T到AB的距离为
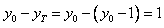 。
。 
练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 (2012•西城区一模)如图,已知抛物线y2=x及两点A1(0,y1)和A2(0,y2),其中y1>y2>0.过A1,A2分别作y轴的垂线,交抛物线于B1,B2两点,直线B1B2与y轴交于点A3(0,y3),此时就称A1,A2确定了A3.依此类推,可由A2,A3确定A4,….记An(0,yn),n=1,2,3,….
(2012•西城区一模)如图,已知抛物线y2=x及两点A1(0,y1)和A2(0,y2),其中y1>y2>0.过A1,A2分别作y轴的垂线,交抛物线于B1,B2两点,直线B1B2与y轴交于点A3(0,y3),此时就称A1,A2确定了A3.依此类推,可由A2,A3确定A4,….记An(0,yn),n=1,2,3,…. .
.