题目内容
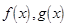 分别为
分别为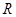 上的奇函数和偶函数,
上的奇函数和偶函数,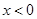 时,
时,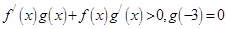 ,则不等式
,则不等式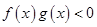 的解集为
的解集为 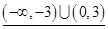
解:因 f’(x)g(x)+f(x)g’(x)>0,即[f(x)g(x)]'>0
故f(x)g(x)在x<0时递增,
又∵f(x),g(x)分别是定义R上的奇函数和偶函数,
∴f(x)g(x)为奇函数,关于原点对称,所以f(x)g(x)在x>0时也是增函数.
∵f(-3)g(-3)=0,∴f(3)g(3)=0
所以f(x)g(x)<0的解集为:x<-3或0<x<3
故答案为:(-∞,-3)∪(0,3)
故f(x)g(x)在x<0时递增,
又∵f(x),g(x)分别是定义R上的奇函数和偶函数,
∴f(x)g(x)为奇函数,关于原点对称,所以f(x)g(x)在x>0时也是增函数.
∵f(-3)g(-3)=0,∴f(3)g(3)=0
所以f(x)g(x)<0的解集为:x<-3或0<x<3
故答案为:(-∞,-3)∪(0,3)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
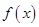 是R上的偶函数,
是R上的偶函数,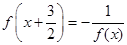 ,在
,在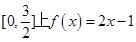 ,则
,则 。
。 对任意
对任意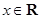 ,都有
,都有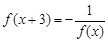 ,且当
,且当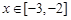 时,
时, ,则
,则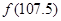 =
= 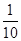

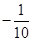
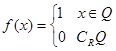 ,则
,则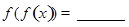 ;下面三个命题中,所有真命题的序号是 .
;下面三个命题中,所有真命题的序号是 . 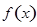 是偶函数;
是偶函数;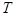 ,
,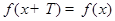 对
对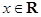 恒成立;
恒成立;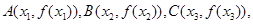 使得
使得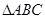 为等边三角形.
为等边三角形.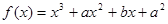 在
在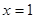 时有极值
时有极值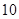 ,则
,则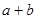 =_______.
=_______.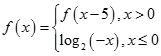 ,则
,则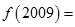 ( )
( )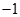
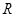 上的函数
上的函数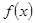 满足
满足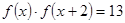 ,若
,若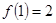 ,则
,则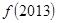 的值为
的值为 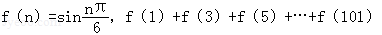 =_________.
=_________.