题目内容
对正整数n,设曲线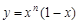 在x=2处的切线与y轴交点的纵坐标为
在x=2处的切线与y轴交点的纵坐标为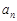 ,则数列
,则数列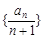 的前n项和的公式是
的前n项和的公式是
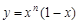 在x=2处的切线与y轴交点的纵坐标为
在x=2处的切线与y轴交点的纵坐标为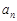 ,则数列
,则数列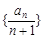 的前n项和的公式是
的前n项和的公式是 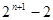
解:∵y'|x=2=-2n-1(n+2),
∴切线方程为:y+2n=-2n-1(n+2)(x-2),
令x=0,求出切线与y轴交点的纵坐标为y0=(n+1)2n,
所以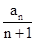 =2n,则数列{
=2n,则数列{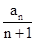 }的前n项和Sn=2(1-2n) 1-2 =2n+1-2
}的前n项和Sn=2(1-2n) 1-2 =2n+1-2
∴切线方程为:y+2n=-2n-1(n+2)(x-2),
令x=0,求出切线与y轴交点的纵坐标为y0=(n+1)2n,
所以
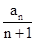 =2n,则数列{
=2n,则数列{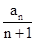 }的前n项和Sn=2(1-2n) 1-2 =2n+1-2
}的前n项和Sn=2(1-2n) 1-2 =2n+1-2
练习册系列答案
相关题目
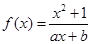 是奇函数,且
是奇函数,且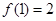 .
. 的表达式;(2) 设
的表达式;(2) 设 ;
; 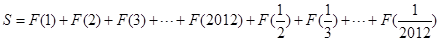 ,求S的值.
,求S的值. 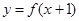 是定义在R上的周期为2的偶函数,当
是定义在R上的周期为2的偶函数,当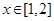 时,
时,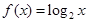 ,设
,设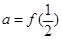 ,
,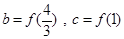 ,则a、b、c的大小关系为( )
,则a、b、c的大小关系为( )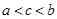
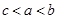
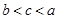
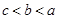
 是
是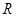 上的奇函数,满足
上的奇函数,满足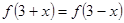 ,当
,当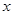 ∈(0,3)时
∈(0,3)时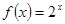
 ,则当
,则当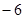 ,
,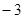 )时,
)时,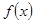 =( )
=( )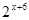
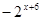
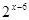
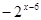
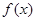 为奇函数,且当
为奇函数,且当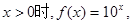 则
则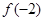 的值是_________
的值是_________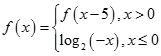 ,则
,则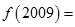 ( )
( )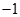
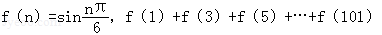 =_________.
=_________.