题目内容
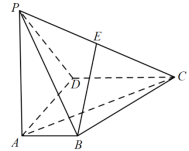
【题目】已知三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为棱
分别为棱![]() 的中点
的中点
(1)求证:![]()
(2)求直线![]() 与
与![]() 所成的角
所成的角
(3)若![]() 为线段
为线段![]() 的中点,
的中点,![]() 在平面
在平面![]() 内的射影为
内的射影为![]() ,求
,求![]()
【答案】(1)见解析;(2)45°;(3)![]() .
.
【解析】
(1)由AC⊥AB,AC⊥AA1即可得出AC⊥平面ABB1A1,于是AC⊥A1B;
(2)以A为原点建立坐标系,求出![]() 和
和 ![]() 的坐标,计算cos
的坐标,计算cos![]() 即可得出直线EF与A1B所成的角;
即可得出直线EF与A1B所成的角;
(3)求出![]() 和平面EFG的法向量
和平面EFG的法向量![]() ,则sin∠HA1A=|cos
,则sin∠HA1A=|cos![]() ,
,![]() |.
|.
(1)∵AA1⊥底面ABC,AC平面ABC
∴AC⊥AA1.
∵∠BAC=90°,∴AC⊥AB.
又A1A平面AA1B1B,AB平面AA1B1B,A1A∩AB=A,
∴AC⊥平面A1ABB1.
∵A1B平面A1ABB1,
∴AC⊥A1B.
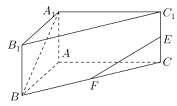
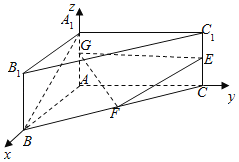
(2)以A为原点建立空间直角坐标系A—xyz,如图所示:
则A1(0,0,1),![]() ,
,![]() ,
,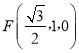 .
.
∴![]() ,
, .
.
∴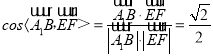 .
.
直线EF与A1B所成的角为45°.
(3)![]() ,
,![]() ,
,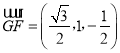 .
.![]() (0,0,1).
(0,0,1).
设平面GEF的法向量为![]() (x,y,z),
(x,y,z),
则 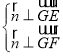 ,∴
,∴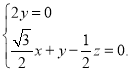
令![]() ,则
,则![]() .
.
∴cos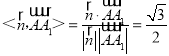 .
.
∵A1在平面EFG内的射影为H,∴∠HA1A为AA1与平面EFG所成的角的余角,
∴cos∠HA1A=|cos![]() |
|![]() .
.
∴∠HA1A![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】垃圾种类可分为可回收垃圾,干垃圾,湿垃圾,有害垃圾,为调查中学生对垃圾分类的了解程度某调查小组随机抽取了某市的![]() 名高中生,请他们指出生活中若干项常见垃圾的种类,把能准确分类不少于
名高中生,请他们指出生活中若干项常见垃圾的种类,把能准确分类不少于![]() 项的称为“比较了解”少于三项的称为“不太了解”调查结果如下:
项的称为“比较了解”少于三项的称为“不太了解”调查结果如下:
|
|
|
|
|
|
| |
男生(人) |
|
|
|
|
|
|
|
女生(人) |
|
|
|
|
|
|
|
(1)完成如下![]() 列联表并判断是否有
列联表并判断是否有![]() 的把握认为了解垃圾分类与性别有关?
的把握认为了解垃圾分类与性别有关?
比较了解 | 不太了解 | 合计 | |
男生 | ________ | ________ | ________ |
女生 | ________ | ________ | ________ |
合计 | ________ | ________ | ________ |
p>
(2)抽取的![]() 名高中生中按照男、女生采用分层抽样的方法抽取
名高中生中按照男、女生采用分层抽样的方法抽取![]() 人的样本.
人的样本.
(i)求抽取的女生和男生的人数;
(ii)从![]() 人的样本中随机抽取两人,求两人都是女生的概率.
人的样本中随机抽取两人,求两人都是女生的概率.
参考数据:
|
|
|
|
|
|
|
|
|
|
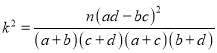 ,
,![]() .
.
【题目】某超市试销某种商品一个月,获得如下数据:
日销售量(件) |
|
|
|
|
|
频率 |
|
|
|
|
|
试销结束后(假设该商品的日销售量的分布规律不变),超市决定正式营销这种商品.设某天超市开始营业时有该商品![]() 件,当天营业结束后检查存货,若发现存货少于
件,当天营业结束后检查存货,若发现存货少于![]() 件,则当天进货补充至
件,则当天进货补充至![]() 件,否则不进货.将频率视为概率.
件,否则不进货.将频率视为概率.
![]() 求当天商品进货的概率.
求当天商品进货的概率.
![]() 记
记![]() 为第二天开始营业时该商品的件数.
为第二天开始营业时该商品的件数.
![]() 求
求![]() 得分布列.
得分布列.
![]() 求
求![]() 得数学期望与方差.
得数学期望与方差.