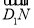题目内容
数列{an}满足an＋1＋(－1)nan＝2n－1，则{an}的前60项和为( )．
A．3 690 B．3 660
C．1 845 D．1 830
D
【解析】∵an＋1＋(－1)nan＝2n－1，
当n＝2k时，a2k＋1＋a2k＝4k－1，
当n＝2k－1时，a2k－a2k－1＝4k－3，
从而a2k＋1＋a2k－1＝2，a2k＋3＋a2k＋1＝2，
因此a2k＋3＝a2k－1，
∴a1＝a5＝a9＝…＝a61，
于是S60＝a1＋a2＋a3＋…＋a60
＝(a2＋a3)＋(a4＋a5)＋…＋(a60＋a61)
＝3＋7＋11＋…＋(2×60－1)＝
＝1 830.
练习册系列答案
相关题目
