题目内容
 分别写在六张卡片上,放在一盒子中。 (1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数卡片则停止抽取,否则继续进行,求抽取次数
分别写在六张卡片上,放在一盒子中。 (1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数卡片则停止抽取,否则继续进行,求抽取次数 的分布列和数学期望.
的分布列和数学期望.(Ⅰ)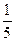 (Ⅱ)
(Ⅱ) 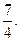
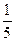 (Ⅱ)
(Ⅱ) 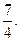
(1)计事件A为“任取两张卡片,将卡片上的函数相加得到的函数是奇函数”,
所以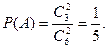 ………5分
………5分
(2) 可取1,2,3,4.
可取1,2,3,4. 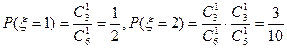 ,
,
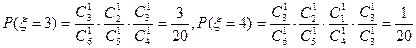 ;…………10分
;…………10分
故ξ的分布列为
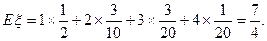 答:
答: 的数学期望为
的数学期望为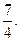 …………13分
…………13分
所以
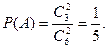 ………5分
………5分(2)
 可取1,2,3,4.
可取1,2,3,4. 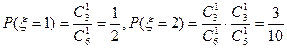 ,
,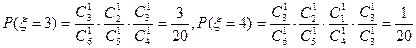 ;…………10分
;…………10分故ξ的分布列为
| ξ | 1 | 2 | 3 | 4 |
| P | 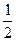 | 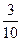 | 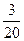 | 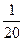 |
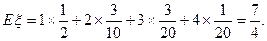 答:
答: 的数学期望为
的数学期望为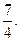 …………13分
…………13分
练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
 名旅客进行服务质量问卷调查,把旅客对住宿的舒适满意度与价格满意度分为五个等级:
名旅客进行服务质量问卷调查,把旅客对住宿的舒适满意度与价格满意度分为五个等级: ,价格满意度
,价格满意度 .
.
 的期望值为
的期望值为 ,求a、b、c的值;
,求a、b、c的值; 。若可通过的信息量
。若可通过的信息量
 表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值.
表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值. 在区间
在区间 上单调递增”为事件A,求事件A的概率.
上单调递增”为事件A,求事件A的概率. ,乙击中目标的概率为
,乙击中目标的概率为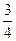 ,每人各射击两发子弹为一个“单位射击组”,若甲击中目标的次数比乙击中目标的次数多,则称此组为“单位进步组”.
,每人各射击两发子弹为一个“单位射击组”,若甲击中目标的次数比乙击中目标的次数多,则称此组为“单位进步组”. ,求
,求 ,第二枪命中率为
,第二枪命中率为 ,该运动员如进行2轮比赛.
,该运动员如进行2轮比赛. ,求
,求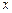
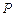
 是随机变量,且
是随机变量,且 ,则
,则 ( ) .
( ) .