题目内容
17.m、n∈R+,mn=2,问2m+4n是否有最值?如有,请求值.分析 直接利用基本不等式求解最值即可.
解答 解:m、n∈R+,mn=2,
2m+4n=2m+22n≥2$\sqrt{{2}^{m}•{z}^{2n}}$=2$\sqrt{{2}^{m+2n}}$=2×${2}^{\frac{m+2n}{2}}$≥2×${2}^{\frac{2\sqrt{2mn}}{2}}$=2×22=8,当且仅当m=2n并且mn=2可得即m=2,n=1取等号.
函数的最小值为:8.
点评 本题考查基本不等式的应用,函数的最小值的求法,考查计算能力.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案
相关题目
7.已知函数f(x)=sin2(ωx)-$\frac{1}{2}$(ω>0)的周期为π,若将其图象沿x轴向右平移a个单位(a>0),所得图象关于原点对称,则实数a的最小值为( )
| A. | π | B. | $\frac{3π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
8.函数f(x)=${log_2}(x+4)-{2^x}$的零点的情况是( )
| A. | 仅有一个或0个零点 | B. | 有两个正零点 | ||
| C. | 有一正零点和一负零点 | D. | 有两个负零点 |
12.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点分别为F1、F2,过F1作倾斜角为30°的直线交双曲线的右支于点P,若∠PF1F2的平分线与∠F1PF2的平分线的交点为Q(1,1),则双曲线的渐近线方程为( )
| A. | y=±$\sqrt{3+2\sqrt{3}}$x | B. | y=±$\sqrt{2\sqrt{3}-3}$x | C. | y=±($\sqrt{3}$+1)x | D. | y=±($\sqrt{3}$-1)x |
6.已知点A(-3,2),B(1,4),P为线段AB的中点,则向量$\overrightarrow{BP}$的坐标为( )
| A. | (-2,-1) | B. | (2,1) | C. | (4,2) | D. | (-8,-4) |
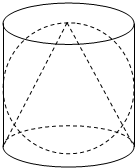 据说伟大的阿基米德死了以后,敌军将领马塞拉斯给他建了一块墓碑.在墓碑上刻了一个如图所示的图案,图案中球的直径与圆柱底面的直径和圆柱的高相等,圆锥的顶点在圆柱上底面的圆心,圆锥的底面是圆柱的下底面.试计算出图形中圆锥、球、圆柱的体积比.
据说伟大的阿基米德死了以后,敌军将领马塞拉斯给他建了一块墓碑.在墓碑上刻了一个如图所示的图案,图案中球的直径与圆柱底面的直径和圆柱的高相等,圆锥的顶点在圆柱上底面的圆心,圆锥的底面是圆柱的下底面.试计算出图形中圆锥、球、圆柱的体积比.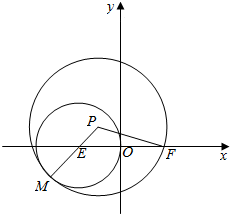 如图,圆E:(x+2)2+y2=4,点F(2,0),动圆P过点F,且与圆E内切于点M,求动圆P的圆心P的轨迹方程.
如图,圆E:(x+2)2+y2=4,点F(2,0),动圆P过点F,且与圆E内切于点M,求动圆P的圆心P的轨迹方程.