题目内容
2.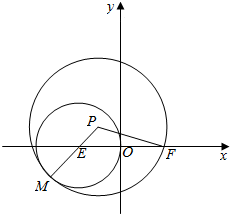 如图,圆E:(x+2)2+y2=4,点F(2,0),动圆P过点F,且与圆E内切于点M,求动圆P的圆心P的轨迹方程.
如图,圆E:(x+2)2+y2=4,点F(2,0),动圆P过点F,且与圆E内切于点M,求动圆P的圆心P的轨迹方程.
分析 利用动圆与圆E内切于点M,|PF|-|PE|=|ME|=2,可得P的轨迹是以E、F为焦点的双曲线的左支,即可求动圆P的圆心P的轨迹方程.
解答 解:∵圆的方程为E:(x+2)2+y2=4,∴圆心为B(-2,0),半径r=2.
设动圆圆心为P(x,y),依题意,
∵动圆与圆E内切于点M,
∴|PF|-|PE|=|ME|=2,
∴P的轨迹是以E、F为焦点的双曲线的左支,其中2a=2,得a=1,
而c=2,∴b2=c2-a2=3,
∴双曲线方程为:x2-$\frac{{y}^{2}}{3}$=1(x≤-1).
点评 本题考查圆与圆的位置关系,考查双曲线的定义域方程,考查学生的计算能力,属于中档题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
12.设集合A,B分别是函数y=log3(9-x2)的定义域和值域,则A∩B=( )
| A. | (-3,2) | B. | (-3,2] | C. | (0,2] | D. | (0,2) |