题目内容
(本小题14分)设函数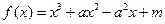
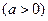
(1)若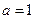 时函数
时函数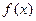 有三个互不相同的零点,求
有三个互不相同的零点,求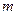 的范围;
的范围;
(2)若函数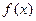 在
在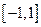 内没有极值点,求
内没有极值点,求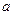 的范围;
的范围;
(3)若对任意的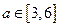 ,不等式
,不等式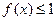 在
在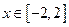 上恒成立,求实数
上恒成立,求实数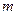 的取值范围.
的取值范围.
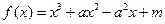
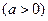
(1)若
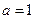 时函数
时函数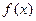 有三个互不相同的零点,求
有三个互不相同的零点,求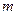 的范围;
的范围;
(2)若函数
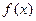 在
在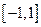 内没有极值点,求
内没有极值点,求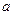 的范围;
的范围;(3)若对任意的
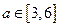 ,不等式
,不等式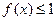 在
在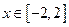 上恒成立,求实数
上恒成立,求实数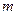 的取值范围.
的取值范围.(1)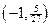
(2)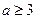
(3)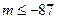
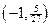
(2)
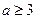
(3)
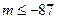
(1)当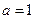 时
时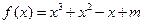 ,
,
因为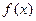 有三个互不相同的零点,所以
有三个互不相同的零点,所以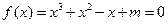 ,
,
即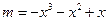 有三个互不相同的实数根。
有三个互不相同的实数根。
令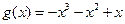 ,则
,则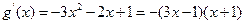 。
。
因为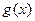 在
在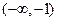 和
和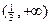 均为减函数,在
均为减函数,在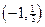 为增函数,
为增函数,
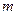 的取值范围
的取值范围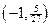
(2)由题可知,方程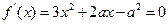 在
在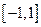 上没有实数根,
上没有实数根,
因为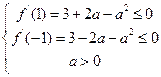 ,所以
,所以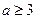
(3)∵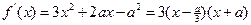 ,且
,且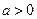 ,
,
∴函数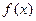 的递减区间为
的递减区间为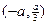 ,递增区间为
,递增区间为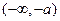 和
和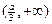 ;
;
当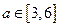 时,
时, 又
又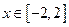 ,
,
∴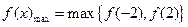 而
而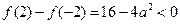
∴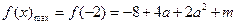 ,
,
又∵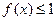 在
在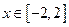 上恒成立,
上恒成立,
∴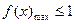 ,即
,即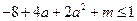 ,即
,即
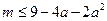 在
在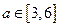 恒
恒 成立。
成立。
∵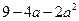 的最小值为
的最小值为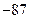
∴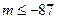
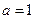 时
时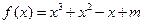 ,
,因为
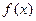 有三个互不相同的零点,所以
有三个互不相同的零点,所以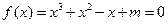 ,
,即
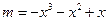 有三个互不相同的实数根。
有三个互不相同的实数根。令
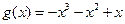 ,则
,则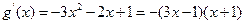 。
。因为
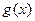 在
在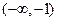 和
和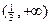 均为减函数,在
均为减函数,在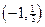 为增函数,
为增函数, 的取值范围
的取值范围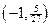
(2)由题可知,方程
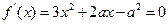 在
在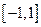 上没有实数根,
上没有实数根,因为
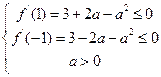 ,所以
,所以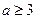
(3)∵
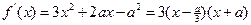 ,且
,且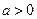 ,
,∴函数
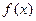 的递减区间为
的递减区间为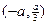 ,递增区间为
,递增区间为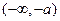 和
和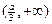 ;
;当
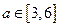 时,
时, 又
又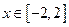 ,
,∴
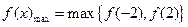 而
而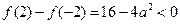
∴
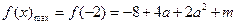 ,
,又∵
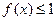 在
在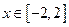 上恒成立,
上恒成立,∴
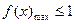 ,即
,即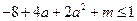 ,即
,即
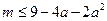 在
在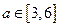 恒
恒 成立。
成立。∵
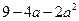 的最小值为
的最小值为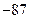
∴
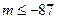

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
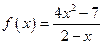 ,
,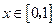 .
.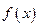 的最值;
的最值;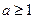 ,函数
,函数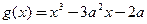 ,
,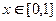 ;若对于任意
;若对于任意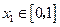 ,总存在
,总存在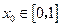 ,使得
,使得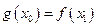 成立,求
成立,求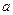 的取值范围
的取值范围
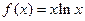 .(Ⅰ)求
.(Ⅰ)求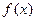 的最小值;
的最小值;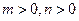 时,求证:
时,求证: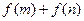 ≥
≥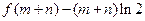 .
.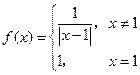 ,若关于
,若关于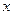 的方程
的方程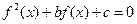
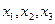 ,则
,则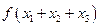 等于_______.
等于_______.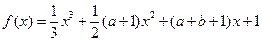 ,若方程
,若方程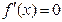 的两个实数根可以分别作为一个椭圆和双曲线的离心率,则
的两个实数根可以分别作为一个椭圆和双曲线的离心率,则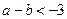
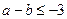
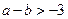
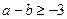
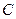 与产量
与产量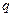 的函数关系式为
的函数关系式为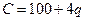
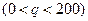 ,价格
,价格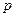 与产量
与产量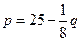 ,求产量
,求产量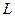 最大。
最大。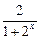 )+asinx+3(a、b为常数),若f(x)在(0,+∞)上有最大值10,则f(x)在(-∞,0)上的最小值是
)+asinx+3(a、b为常数),若f(x)在(0,+∞)上有最大值10,则f(x)在(-∞,0)上的最小值是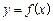 的图象如左下图所示,则函数
的图象如左下图所示,则函数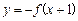 的图象大致为
的图象大致为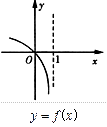

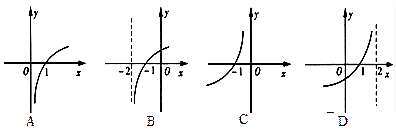

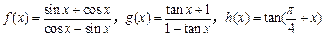 ,下列是同一函数的是( )
,下列是同一函数的是( ) 与
与