题目内容
正方体ABCD-A1B1C1D1中,E、F分别是AA1与CC1的中点,则直线ED与D1F所成角的余弦值是( )
分析:先建立空间直角坐标系,分别写出相关点和相关向量的坐标,再利用向量数量积运算的夹角公式计算两直线方向向量的夹角余弦值,由于异面直线所成的角的范围为(0,90°],故直线ED与D1F所成角的余弦值应为非负数
解答:解:如图:以D为原点,DA、DF、DD1为x、y、z轴建立空间直角坐标系,设正方体的边长为2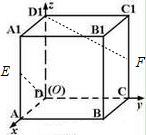
则D(0,0,0),E(2,0,1),F(0,2,1),D1(0,0,2)
∴
=(2,0,1),
=(0,2,-1)
cos<
,
>=
=
=-
∴直线ED与D1F所成角的余弦值为|cos<
,
>|=
故选 A

则D(0,0,0),E(2,0,1),F(0,2,1),D1(0,0,2)
∴
| DE |
| D1F |
cos<
| DE |
| D1F |
| ||||
|
|
| -1 | ||||
|
| 1 |
| 5 |
∴直线ED与D1F所成角的余弦值为|cos<
| DE |
| D1F |
| 1 |
| 5 |
故选 A
点评:本题考查了空间异面直线所成的角的求法,空间直角坐标系在解决空间线线角问题中的应用,向量数量积运算及夹角公式的运用.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的:
如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的: 已知边长为6的正方体ABCD-A1B1C1D1,E,F为AD、CD上靠近D的三等分点,H为BB1上靠近B的三等分点,G是EF的中点.
已知边长为6的正方体ABCD-A1B1C1D1,E,F为AD、CD上靠近D的三等分点,H为BB1上靠近B的三等分点,G是EF的中点. 如图所示,在棱长为2cm的正方体ABCD-A1B1C1D1中,A1B1的中点是P,过点A1作出与截面PBC1平行的截面,简单证明截面形状,并求该截面的面积.
如图所示,在棱长为2cm的正方体ABCD-A1B1C1D1中,A1B1的中点是P,过点A1作出与截面PBC1平行的截面,简单证明截面形状,并求该截面的面积. 如图,正方体ABCD-A1B1C1D1中,M是棱AB的中点,过A1,M,C三点的平面与CD所成角正弦值( )
如图,正方体ABCD-A1B1C1D1中,M是棱AB的中点,过A1,M,C三点的平面与CD所成角正弦值( )