题目内容
12.若集合A=$\left\{{({x,y})\left|{\frac{x^2}{2}+{y^2}<1}\right.}\right\},B=\left\{{({x,y})\left|{x∈Z,y∈Z}\right.}\right\}$,则A∩B的元素个数为3.分析 集合A表示长轴为$\sqrt{2}$,短轴为1的椭圆内部的点集,B表示整数集,画出相应的图形,如图所示,找出A∩B的元素个数即可.
解答  解:如图所示,
解:如图所示,
由图形得:A∩B={(0,0),(-1,0),(1,0)},共3个元素.
故答案为:3.
点评 此题考查了交集及其运算,利用了数形结合的思想,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
3.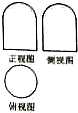 一个几何体的三视图如图,正视图和俯视图都是由一个边长为2的正方形组成,俯视图是一个圆,则这个几何体的表面积为( )
一个几何体的三视图如图,正视图和俯视图都是由一个边长为2的正方形组成,俯视图是一个圆,则这个几何体的表面积为( )
 一个几何体的三视图如图,正视图和俯视图都是由一个边长为2的正方形组成,俯视图是一个圆,则这个几何体的表面积为( )
一个几何体的三视图如图,正视图和俯视图都是由一个边长为2的正方形组成,俯视图是一个圆,则这个几何体的表面积为( )| A. | 5π | B. | 6π | C. | 7π | D. | 9π |
1.已知x,y,z,a∈R,且x2+4y2+z2=6,则使不等式x+2y+3z≤a恒成立的a的最小值为( )
| A. | 6 | B. | $\sqrt{66}$ | C. | 8 | D. | $\sqrt{88}$ |