题目内容
(本题满分12分)已知函数f(x)=lg(2+x),g(x)=lg(2-x),设h(x)=f(x)+g(x).
(1)求函数h(x)的定义域;
(2)判断函数h(x)的奇偶性,并说明理由.
(1)求函数h(x)的定义域;
(2)判断函数h(x)的奇偶性,并说明理由.
解(1)由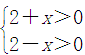 得-2<x<2.所以函数h(x)的定义域是{x|-2<x<2}.
得-2<x<2.所以函数h(x)的定义域是{x|-2<x<2}.
(2) ∵h(-x)=lg(2-x)+lg(2+x)=h(x),∴h(x)是偶函数.
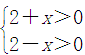 得-2<x<2.所以函数h(x)的定义域是{x|-2<x<2}.
得-2<x<2.所以函数h(x)的定义域是{x|-2<x<2}. (2) ∵h(-x)=lg(2-x)+lg(2+x)=h(x),∴h(x)是偶函数.
略

练习册系列答案
相关题目
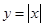
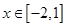 ,求函数的最小值与最大值
,求函数的最小值与最大值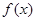 是定义在R上的奇函数,若当
是定义在R上的奇函数,若当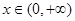 时,
时,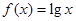 ,则满足
,则满足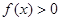 的
的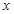 的取值范围是( )
的取值范围是( )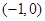
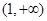
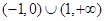
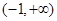
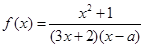 为偶函数,则
为偶函数,则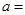 ( ).
( ).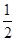

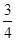
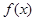 为偶函数,且当
为偶函数,且当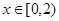 时
时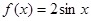 ,当
,当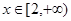 时
时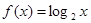 ,则
,则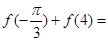 ( )
( )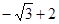

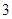

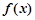 是偶函数,当
是偶函数,当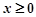 时,
时, 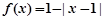 ,满足
,满足 的实数
的实数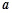 的个数为_____________个
的个数为_____________个 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当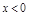 时,
时,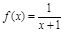 ,则
,则 =
= 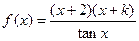 为奇函数,则
为奇函数,则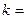
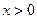 时,
时,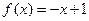 ;则当
;则当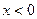 时,f(x)的解析式为_______________.
时,f(x)的解析式为_______________.