题目内容
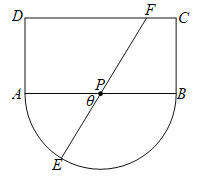
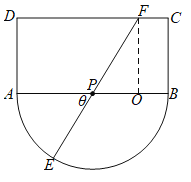
【题目】某农业观光区的平面示意图如图所示,其中矩形![]() 的长
的长![]() 千米,宽
千米,宽![]() 千米,半圆的圆心
千米,半圆的圆心![]() 为
为![]() 中点,为了便于游客观光休闲,在观光区铺设一条由圆弧
中点,为了便于游客观光休闲,在观光区铺设一条由圆弧![]() 、线段
、线段![]() 、
、![]() 组成的观光道路,其中线段
组成的观光道路,其中线段![]() 经过圆心
经过圆心![]() ,点
,点![]() 在线段
在线段![]() 上(不含线段端点
上(不含线段端点![]() 、
、![]() ),已知道路
),已知道路![]() 、
、![]() 的造价为每千米
的造价为每千米![]() 万元,道路
万元,道路![]() 造价为每千米
造价为每千米![]() 万元,设
万元,设![]() ,观光道路的总造价为
,观光道路的总造价为![]() .
.
(1)试求![]() 与
与![]() 的函数关系式
的函数关系式![]() ,并写出
,并写出![]() 的取值范围;
的取值范围;
(2)当![]() 为何值时,观光道路的总造价
为何值时,观光道路的总造价![]() 最小.
最小.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由题意可知![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,则
,则![]() ,求出
,求出![]() 、
、![]() ,即可求出
,即可求出![]() 与
与![]() 的函数关系式
的函数关系式![]() ;
;
(2)求导数,确定函数的单调性,即可得出当![]() 为何值时,观光道路的总造价
为何值时,观光道路的总造价![]() 最小.
最小.
(1)由题意可知![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,则
,则![]() ,
,
则![]() ,
,![]() ,
,
因此,![]() ,其中
,其中![]() ;
;
(2)![]()
![]() ,
,
令![]() ,得
,得![]() ,列表如下:
,列表如下:
|
|
|
|
|
|
|
|
|
| 极大值 |
|
所以,函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
因此,当![]() 时,观光道路的总造价最小.
时,观光道路的总造价最小.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目