Question

【题目】四棱锥P-ABCD的底面是边长为2的正方形，PA⊥平面ABCD，E，F分别为线段AB，BC的中点．

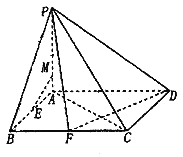
（1）线段AP上一点M，满足，求证：EM∥平面PDF；

（2）若PB与平面ABCD所成的角为45°，求二面角A-PD-F的余弦值．

Answer 1

【答案】（1）见解析（2）

【解析】

（1）建立空间直角坐标系，利用·=0，即可证明EM∥平面PDF；

（2）求出平面PDF和平面PAD的一个法向量，利用向量的夹角公式，即可求解二面角的余弦值．

（1）由题意，以A为原点，AB为x轴，AD为y轴，AP为z轴，建立空间直角坐标系，

设PA=a，则A（0，0，0），M（0，0，），P（0，0，a），F（2，1，0），D（0，2，0），

E（1，0，0），所以=（-1，0，），=（2，1，-a），=（0，2，-a），

设平面PDF的法向量=（x，y，z），

则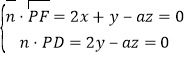，取z=2，得=（，a，2），

∵·=-+2×=0，EM平面PDF，∴EM∥平面PDF．

（2）因为PB与平面ABCD所成的角为45°，可得PA=AB=2，

所以P（0，0，2），D（0，2，0），F（2，1，0），

所以=（0，2，-2），=（2，1，0），

设平面PDF的法向量为=（x，y，z），

则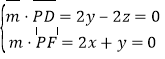，取y=1，得=（，1，1），

又由平面PAD的法向量=（1，0，0），

设二面角A-PD-F的平面角为θ，则，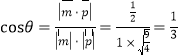

∴二面角A-PD-F的余弦值为．