题目内容
7.师大附中三年级一班40人随机平均分成两组,两组学生一次考试的成绩情况如下表:| 统计量 组别 | 平均成绩 | 标准差 |
| 第一组 | 90 | 6 |
| 第二组 | 80 | 4 |
分析 因为是平均分组,所以全班学生的平均值是两组学生平均值的平均,标准差计算时要分开算出每组学生对全班平均值的差的平方和,再求标准差.
解答 解:∵某班40人随机平均分成两组,
两个组的平均成绩分别是80,90.
∴全班的平均成绩是:$\frac{80×20+90×20}{40}$=85,
由已知$\frac{1}{20}$$\sum_{1}^{20}$(xi-90)2=36,即$\sum_{i=1}^{20}$(xi-90)2=720,
即$\sum_{i=1}^{20}$(xi-85-5)2=720,即$\sum_{i=1}^{20}$(xi-85)2-10$\sum_{i=1}^{20}$(xi-85)+500=720
$\frac{1}{20}$$\sum_{i=1}^{20}$(xj-80)2=16,即$\sum_{j=1}^{20}$(xj-85+5)2=320,即$\sum_{j=1}^{20}$(xj-85)2+10$\sum_{j=1}^{20}$(xj-85)+500=320,
故$\sum_{i=1}^{20}$(xi-85)2+$\sum_{j=1}^{20}$(xj-85)2-10$\sum_{i=1}^{20}$(xi-85)+10$\sum_{j=1}^{20}$(xj-85)+1000=1040,
故$\sum_{i=1}^{20}$(xi-85)2+$\sum_{j=1}^{20}$(xj-85)2-10$\sum_{i=1}^{20}$xi+10$\sum_{j=1}^{20}$xj+1000=2040
故$\sum_{i=1}^{20}$(xi-85)2+$\sum_{j=1}^{20}$(xj-85)2=2040
故$\sum_{i=1}^{40}$(xi-85)2=2040
∴S=$\sqrt{\frac{1}{40}×2040}$=$\sqrt{51}$.
∴全班学生的平均成绩为85,标准差为$\sqrt{51}$.
点评 本题考点是方差与标准差,本题属于变换求标准差的题型,关键是厘清相关数据之间的关系,达到用已知表示未知的目的,请认真体会本题的转化方法,其本质是作了一系列的恒等变形.

 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案| A. | 4条 | B. | 3条 | C. | 2条 | D. | 无数条 |
| A. | a≥-2 | B. | a≤-2 | C. | a≥5 | D. | a≤5 |
| A. | $\frac{5}{2}$-$\frac{2n+5}{{2}^{n+1}}$ | B. | 5-$\frac{2n+5}{{2}^{n}}$ | C. | $\frac{2n+1}{{2}^{n}}+1$ | D. | $\frac{2n+5}{{2}^{n}}$-1 |
| A. | 大于0 | B. | 小于0 | C. | 等于0 | D. | 不确定 |
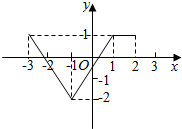 根据如图所示的函数y=f(x)的图象,写出函数的解析式.
根据如图所示的函数y=f(x)的图象,写出函数的解析式.