题目内容
【题目】各项均为正数的数列{bn}的前n项和为Sn , 且对任意正整数n,都有2Sn=bn(bn+1).
(1)求数列{bn}的通项公式;
(2)如果等比数列{an}共有2015项,其首项与公比均为2,在数列{an}的每相邻两项ak与ak+1之间插入k个(﹣1)kbk(k∈N*)后,得到一个新的数列{cn}.求数列{cn}中所有项的和;
(3)如果存在n∈N* , 使不等式 ![]() 成立,求实数λ的范围.
成立,求实数λ的范围.
【答案】
(1)解:当n=1时,由2S1=b1(b1+1)得b1=1,
当n≥2时,由2Sn=bn(bn+1),2Sn﹣1=bn﹣1(bn﹣1+1)得(bn+bn﹣1)(bn﹣bn﹣1)=bn+bn﹣1
因数列{bn}的各项均为正数,所以bn﹣bn﹣1=1,
所以数列{bn}是首项与公差均为1的等差数列,
所以数列{bn}的通项公式为bn=n.
(2)解:数列{an}的通项公式为 ![]() ,
,
数列{cn}共有2015+1+2+…+2014=1008×2015项,
其所有项的和为S1008×2015=(2+22+…+22015)+(﹣1+22﹣32+42﹣…20132+20142)
=2(22015﹣1)+[3+7+…+4027]=22016﹣2+ ![]() ×1007
×1007
=22016+2015×1007﹣2=22016+2029103
(3)解:由 ![]() ,
,
得 ![]() ,
,
记 ![]()
因为 ![]() ,当
,当 ![]() 取等号,所以
取等号,所以 ![]() 取不到
取不到 ![]() ,
,
当n=3时, ![]() 的最小值为
的最小值为 ![]()
![]() (n∈N*)递减,
(n∈N*)递减,
![]() 的最大值为B1=6,
的最大值为B1=6,
所以如果存在n∈N*,使不等式 ![]() 成立
成立
实数λ应满足A3≤λ≤B1,即实数λ的范围应为 ![]()
【解析】
【考点精析】关于本题考查的数列的前n项和,需要了解数列{an}的前n项和sn与通项an的关系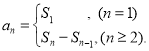 才能得出正确答案.
才能得出正确答案.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目