Question

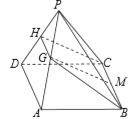
【题目】如图，在四棱锥中，底面为矩形，为等边三角形，且平面平面.为的中点，为的中点，过点，，的平面交于.

（1）求证：平面；

（2）若时，求二面角的余弦值.

Answer 1

【答案】(1)证明见解析；(2)

【解析】

（1）首先证明平面，由平面平面，可说明，由此可得四边形为平行四边形，即可证明平面；

（2）延长交于点，过点作交直线于点，则即为二面角的平面角，求出的余弦值即可得到答案。

（1）∵为矩形

∴，平面，平面

∴平面.

又因为平面平面，

∴.

为中点，为中点，

所以平行且等于，即四边形为平行四边形

所以，平面，平面

所以平面

（2）不妨设，.

因为为中点，为等边三角形，所以，，且

∵，所以有平面，故

因为平面平面

∴平面，又，

∴平面，则

延长交于点，过点作交直线于点，

由于平行且等于，所以为中点，，

由于，，，所以平面，则，

所以即为二面角的平面角

在中，，，

所以，

所以.