题目内容
、(本小题12分)
设函数
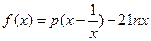 ,
,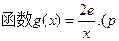 是实数,
是实数,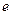 是自然对数的底数)
是自然对数的底数)(1)当
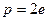 时,求
时,求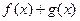 的单调区间;
的单调区间;(2)若直线
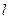 与函数
与函数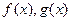 的图象都相切,且与函数
的图象都相切,且与函数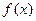 的图象相切于点(1,0),求P的值。
的图象相切于点(1,0),求P的值。解:(1)当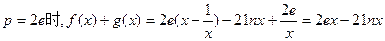
则 ……………………………………………………(2分)
……………………………………………………(2分)
故当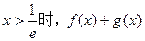 是增函数;
是增函数;
当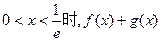 是减函数,……………………………………(4分)
是减函数,……………………………………(4分)
综上,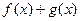 的单调增区间为
的单调增区间为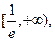
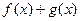 的单调减区间为
的单调减区间为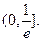 …………………………………………(6分)
…………………………………………(6分)
(2)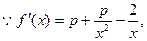
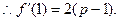
设直线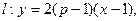 ………………………………………………(8分)
………………………………………………(8分)
由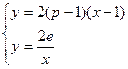 得
得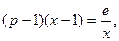
即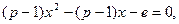 …………………………………………(10分)
…………………………………………(10分)
当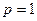 时,方程无解;
时,方程无解;
当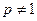 时,
时,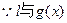 图象相切,
图象相切,
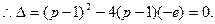
得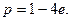
综上,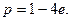 ………………………………………………………(12分)
………………………………………………………(12分)
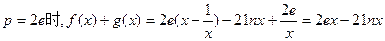
则
 ……………………………………………………(2分)
……………………………………………………(2分)故当
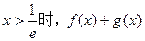 是增函数;
是增函数;当
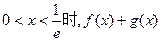 是减函数,……………………………………(4分)
是减函数,……………………………………(4分)综上,
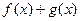 的单调增区间为
的单调增区间为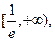
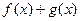 的单调减区间为
的单调减区间为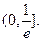 …………………………………………(6分)
…………………………………………(6分)(2)
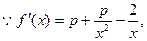
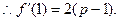
设直线
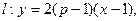 ………………………………………………(8分)
………………………………………………(8分)由
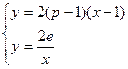 得
得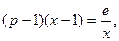
即
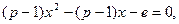 …………………………………………(10分)
…………………………………………(10分)当
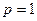 时,方程无解;
时,方程无解;当
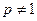 时,
时,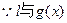 图象相切,
图象相切,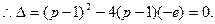
得
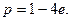
综上,
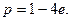 ………………………………………………………(12分)
………………………………………………………(12分)略

练习册系列答案
相关题目
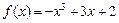 分别在
分别在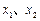 处取得极小值、极大值.
处取得极小值、极大值.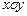 平面上点
平面上点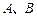 的坐标分别为
的坐标分别为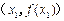 、
、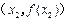 ,该平面上动点
,该平面上动点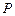 满足
满足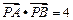 ,点
,点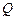 是点
是点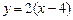 的对称点,.求
的对称点,.求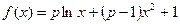 .
.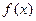 的单调性;
的单调性;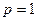 时,
时,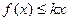 恒成立,求实数
恒成立,求实数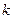 的取值范围;
的取值范围;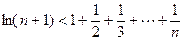
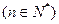 .
. (x)= ( )
(x)= ( )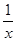 +1
+1 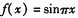 是[0,1]上的函数,且定义
是[0,1]上的函数,且定义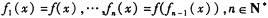 ,则满足
,则满足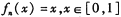 的x的个数是
的x的个数是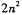
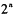
 与
与 所围成的图形的面积是
所围成的图形的面积是  。
。 的图象过点P( 1,2),且在点P处的切线与直线x-3y=0垂直.
的图象过点P( 1,2),且在点P处的切线与直线x-3y=0垂直.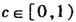 ,试求函数f(x)的单调区间;
,试求函数f(x)的单调区间; ,m),(n,
,m),(n,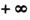 )是f(x)的单调递
)是f(x)的单调递 增区间,试求n-m-2c的范围
增区间,试求n-m-2c的范围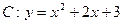 上的点,且曲线C在点P处切线倾倾角的取值范围为
上的点,且曲线C在点P处切线倾倾角的取值范围为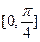 ,则点P横坐标的取值范围为( )
,则点P横坐标的取值范围为( )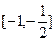
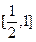
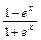 的导数为 .
的导数为 .