题目内容
已知圆
与直线
及
都相切，圆心在直线
上，则圆的方程为（ ）
A． | B． |
C． | D． |
B
解析试题分析:（法一）根据答案中的选项得出圆心和半径，分别代入验证即可.
（法二）依题意设圆心为
，半径为
，因为圆与直线及都相切，所以
，解得
所以圆心为
，进而可求得
考点：本小题考查圆的方程的求法.
点评：对于已知直线与圆相切的问题，首先要用圆心到直线的距离等于圆半径，这样可以简化运算.
练习册系列答案
新编小学单元自测题系列答案
字词句段篇系列答案
相关题目
两圆相交于点
,两圆的圆心均在直线
上，则
的值为（ ）
A． | B． | C． | D． |
若点P（1，1）为圆
的弦MN的中点，则弦MN所在直线的方程为（ ）
A． | B． |
C． | D． |
直线
绕原点按顺时针方向旋转
所得直线与圆
的位置关系是（ ）.
| A．直线与圆相切 | B．直线与圆相交但不过圆心 |
| C．直线与圆相离 | D．直线过圆心 |
直线
与圆
的位置关系是 （ ）
| A．相切 | B．相交但直线不过圆心 | C．直线过圆心 | D．相离 |
圆
上的点到直线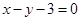
的距离的最大值是（ ）
A． | B． | C． | D．0 |
圆
与圆
的位置关系是（ ）
| A．相离 | B．内含 | C．外切 | D．内切 |
以下叙述正确的是（ ）
| A．平面直角坐标系下的每条直线一定有倾斜角与法向量，但是不一定都有斜率； |
| B．平面上到两个定点的距离之和为同一个常数的轨迹一定是椭圆； |
C．直线 上有且仅有三个点到圆 的距离为2； |
D．点 是圆 上的任意一点，动点 分 （ 为坐标原点）的比为 ，那么的轨迹是有可能是椭圆. |
点M(x0,y0)是圆x2+y2=a2 (a>0)内不为圆心的一点，则直线x0x+y0y=a2与该圆的位置关系是（ ）
| A．相切 | B．相交 | C．相离 | D．相切或相交 |