题目内容
(本题满分16分)
已知数列{an}满足Sn+an=2n+1,
(1) 写出a1, a2, a3,并推测an的表达式;
(2) 用数学归纳法证明所得的结论。
【答案】
(1) a1=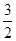 , a2=
, a2=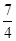 , a3=
, a3=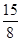 , 猜测 an=2-
, 猜测 an=2-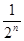 (2)见解析
(2)见解析
【解析】解: (1) a1=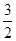 , a2=
, a2=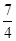 , a3=
, a3=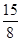 , 猜测 an=2-
, 猜测 an=2-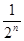 ……5分
……5分
(2) ①由(1)已得当n=1时,命题成立;……8分
②假设n=k时,命题成立,即 ak=2-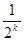 , ……10分
, ……10分
当n=k+1时, a1+a2+……+ak+ak+1+ak+1=2(k+1)+1,且a1+a2+……+ak=2k+1-ak
∴2k+1-ak+2ak+1=2(k+1)+1=2k+3,
∴2ak+1=2+2-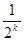 , ak+1=2-
, ak+1=2-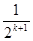 , 即当n=k+1时,命题成立. ……15分
, 即当n=k+1时,命题成立. ……15分
根据①②得n∈N+ , an=2-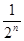 都成立
……16分
都成立
……16分
思路分析:第一问利用Sn+an=2n+1,递推得到a1=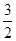 , a2=
, a2=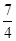 , a3=
, a3=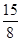 , 猜测 an=2-
, 猜测 an=2-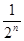
第二问中,1)已得当n=1时,命题成立;
②假设n=k时,命题成立,即 ak=2-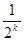 ,当n=k+1时, a1+a2+……+ak+ak+1+ak+1=2(k+1)+1,且a1+a2+……+ak=2k+1-ak
,当n=k+1时, a1+a2+……+ak+ak+1+ak+1=2(k+1)+1,且a1+a2+……+ak=2k+1-ak
∴2k+1-ak+2ak+1=2(k+1)+1=2k+3,
∴2ak+1=2+2-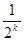 , ak+1=2-
, ak+1=2-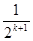
综上可知成立。

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目


 在
在 上的单调性;
上的单调性; ,使
,使 ,则称
,则称 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求 的值;
的值; 在
在