题目内容
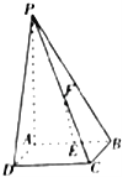
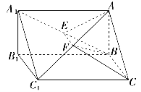
【题目】如(1)图所示,在直角梯形ABCD中,AD∥BC,![]() ,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图(2)所示.
,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图(2)所示.
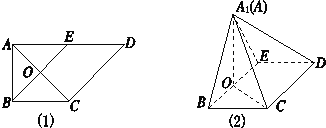
(1)证明:CD⊥平面A1OC;
(2)若平面A1BE⊥平面BCDE,求平面A1BC与平面A1CD所成锐二面角的余弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
试题分析:(1)要证明直线![]() 与平面
与平面![]() 垂直,在直角梯形
垂直,在直角梯形![]() 中易得
中易得![]() ,因此只要能证
,因此只要能证![]() 与此平面垂直即可,而同样在梯形中
与此平面垂直即可,而同样在梯形中![]() ,折叠时,垂直保持不变,因此易得垂直结论;(2)由已知平面A1BE⊥平面BCDE,则可以以O为原点,OB,OC,OA1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,从而写出各点坐标,求出平面
,折叠时,垂直保持不变,因此易得垂直结论;(2)由已知平面A1BE⊥平面BCDE,则可以以O为原点,OB,OC,OA1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,从而写出各点坐标,求出平面![]() 和平面
和平面![]() 的法向量,由法向量的夹角得二面角.
的法向量,由法向量的夹角得二面角.
试题解析:(1)证明:在图(1)中,
因为AB=BC=1,AD=2,E是AD的中点,
![]() ,所以BE⊥AC,BE∥CD.
,所以BE⊥AC,BE∥CD.
即在图(2)中,BE⊥OA1,BE⊥OC,
又OA1∩OC=O,OA1![]() 平面A1OC,OC
平面A1OC,OC![]() 平面A1OC,
平面A1OC,
从而BE⊥平面A1OC.
又CD∥BE,
所以CD⊥平面A1OC.
(2)由已知,平面A1BE⊥平面BCDE,
又由(1)知,BE⊥OA1,BE⊥OC,
所以∠A1OC为二面角A1BE C的平面角,
所以![]()
如图,以O为原点,OB,OC,OA1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,
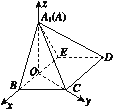
因为A1B=A1E=BC=ED=1,BC∥ED,
所以![]()
![]() ,
,![]() ,
,![]()
得![]() ,
,![]()
![]()
设平面A1BC的法向量n1=(x1,y1,z1),平面A1CD的法向量n2=(x2,y2,z2)
则![]() 得
得![]() 取n1=(1,1,1);
取n1=(1,1,1);
![]() 得
得![]() 取n2=(0,1,1),
取n2=(0,1,1),
从而![]()
即平面A1BC与平面A1CD所成锐二面角的余弦值为![]()

练习册系列答案
相关题目