题目内容
【题目】如图,四棱锥P﹣ABCD的底面是边长为1的正方形,PA⊥底面ABCD,E、F分别为AB、PC的中点.
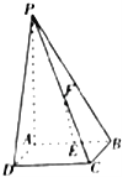
(Ⅰ)求证:EF∥平面PAD;
(Ⅱ)若PA=2,试问在线段EF上是否存在点Q,使得二面角Q﹣AP﹣D的余弦值为![]() ?若存在,确定点Q的位置;若不存在,请说明理由.
?若存在,确定点Q的位置;若不存在,请说明理由.
【答案】(I)证明见解析;(II)满足条件的![]() 存在,是
存在,是![]() 中点.
中点.
【解析】
试题分析:本题考查二面角,空间中线面的位置关系,向量数量积运算,注意解题方法的积累,建立坐标系是解决本题的关键,属于中档题,考查学生的分析问题解决问题的能力、空间想象能力、逻辑推理能力、计算能力.第一问,取![]() 中点
中点![]() ,连接
,连接![]() ,通过中位线定理可得
,通过中位线定理可得![]() ,利用线面平行的判定定理即得结论;第二问,以点
,利用线面平行的判定定理即得结论;第二问,以点![]() 为坐标原点建立空间直角坐标系,则平面
为坐标原点建立空间直角坐标系,则平面![]() 的法向量与平面
的法向量与平面![]() 的法向量的夹角的余弦值即为
的法向量的夹角的余弦值即为![]() ,计算即可.
,计算即可.
试题解析:证明:(Ⅰ)取![]() 中点
中点![]() ,连接
,连接![]() ,在
,在![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]()
![]() ,正方形
,正方形![]() 中
中![]() 为
为![]() 中点,
中点,![]()
![]() ,
,![]()
![]() ,故四边形
,故四边形![]() 为平行四边形,
为平行四边形,![]()
![]() ,
,
又![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
, ![]()
![]() 平面
平面![]() ;
;
(Ⅱ)结论:满足条件的![]() 存在,是
存在,是![]() 中点.理由如下:如图:以点
中点.理由如下:如图:以点![]() 为坐标原点建立空间直角坐标系,
为坐标原点建立空间直角坐标系,
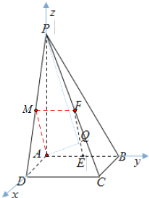
则![]() ,由题易知平面
,由题易知平面![]() 的法向量为
的法向量为![]() ,假设存在
,假设存在![]() 满足条件:设
满足条件:设![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,
,
由 ,可得
,可得![]() ,
,
![]()
![]() ,
,
由已知:![]() ,解得:
,解得:![]() ,
,
所以满足条件的![]() 存在,是
存在,是![]() 中点.
中点.

练习册系列答案
相关题目