题目内容
9．设集合U={1，2，3，4}，A={1，2}，B={2，4}，则B∩（∁UA）=（ ）| A． | {2} | B． | {4} | C． | {1，2，4} | D． | {1，4} |
分析 根据题意，先求出A的补集∁UA，再由交集的意义，计算可得（∁UA）∩B，即可得答案
解答 解：根据题意，集合U={1，2，3，4}，A={1，2}，
则∁UA={3，4}，
又由B={2，4}，
则（∁UA）∩B={4}；
故选：B．
点评 本题考查集合混合运算，注意运算的顺序，其次要理解集合交、并、补的含义．
练习册系列答案
相关题目
17．
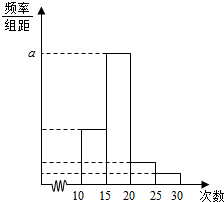对某校高一年级学生参加“社区志愿者”活动次数进行统计，随机抽取M名学生作为样本，得到这M个学生参加“社区志愿者”活动的次数．据此作出频数和频率统计表及频率分布直方图如下：
（Ⅰ）求出表中M，p及图中a的值；
（Ⅱ）若该校高一学生有720人，试估计他们参加“社区志愿者”活动的次数在[15，20）内的人数；
（Ⅲ）若参加“社区志愿者”活动的次数不少于20次的学生可评为“优秀志愿者”，试估计小明被评为“优秀志愿者”的概率．
对某校高一年级学生参加“社区志愿者”活动次数进行统计，随机抽取M名学生作为样本，得到这M个学生参加“社区志愿者”活动的次数．据此作出频数和频率统计表及频率分布直方图如下：| 分组 | 频数 | 频率 |
| [10，15） | 5 | 0.25 |
| [15，20） | 12 | n |
| [20，25） | m | p |
| [25，30] | 1 | 0.05 |
| 合计 | M | 1 |
（Ⅱ）若该校高一学生有720人，试估计他们参加“社区志愿者”活动的次数在[15，20）内的人数；
（Ⅲ）若参加“社区志愿者”活动的次数不少于20次的学生可评为“优秀志愿者”，试估计小明被评为“优秀志愿者”的概率．
14．设集合A={x|x2-9＜0}，B={x|-1＜x≤5}，则A∩B=（ ）
| A． | （-3，-1） | B． | （-3，5] | C． | （3，5] | D． | （-1，3） |
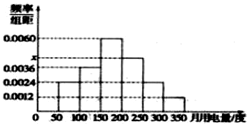利用简单随机抽样从某小区抽取100户居民进行月用电量调查，发现其用电量都在50到350度之间，频率分布直方图如图所示．在这些用户中，用电量落在区间[150，250]内的户数为（ ）