题目内容
5. 如图,在△ABC中,G为重心,在AD的延长线上取一点G′,使得GD=G′D=4,若CG=6,BG=10,求△ABC的面积.
如图,在△ABC中,G为重心,在AD的延长线上取一点G′,使得GD=G′D=4,若CG=6,BG=10,求△ABC的面积.
分析 利用三角形重心的性质得到三角形AGF,BFG,CDG,BDG的面积与三角形ACG面积的关系即可.
解答 解:由题意,BC与GG'互相平分,所以四边形BGCG'为平行四边形,所以BG'=CG=6,GG'=8,CG=10,所以CG⊥GG',又在△ABC中,G为重心,所以${S}_{△ACG}=2{S}_{△CDG}=\frac{1}{2}AG×CG$=$\frac{1}{2}×8×6$=24,
${S}_{△AFG}=\frac{1}{2}AG×GF$=$\frac{1}{2}×8×3$=12,
GF=3=$\frac{1}{2}$BG',所以${S}_{△GFB}=\frac{1}{2}{S}_{△BGG'}=\frac{1}{2}×\frac{1}{2}GG'×BG'$=$\frac{1}{2}×\frac{1}{2}×8×6$=12,所以${S}_{△BDG}=\frac{1}{2}{S}_{△BGG'}$=12,
所以△ABC的面积为S△ACG+S△AFG+S△CDG+S△BDG+S△GFB=24+12+12+12+12=72.
点评 本题考查了三角形面积的求法,关键是三角形重心性质的运用.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 则
则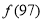 的值为( )
的值为( )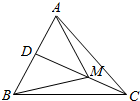
 如图,给出16个点,其左和右相邻两点,上下相邻两点的距离都为1,若以这些点为三角形的顶点,那么一共可得到200个直角三角形.
如图,给出16个点,其左和右相邻两点,上下相邻两点的距离都为1,若以这些点为三角形的顶点,那么一共可得到200个直角三角形.