题目内容

已知直三棱柱ABC-A1B1C1的各棱长均为1，棱BB1所在直线上的动点M满足
BM
=λ
BB1
，AM与侧面BB1C1C所成的角为θ，若λ∈[
2
2
，
2
]，则θ的取值范围是（　　）
分析：取BC中点O，连接AO，MO，可得∠AMO是AM与侧面BB1C1C所成的角，从而可得sinθ=
AO
AM
=
3
2
1+λ2
，结合条件，即可得到结论．
解答：解：取BC中点O，连接AO，MO，则
∵棱柱ABC-A1B1C1是直三棱柱，
∴AO⊥侧面BB1C1C，
∴∠AMO是AM与侧面BB1C1C所成的角
∵直三棱柱ABC-A1B1C1的各棱长均为1，
BM
=λ
BB1
，
∴AO=
3
2
，AM=
1+λ2

∴sinθ=
AO
AM
=
3
2
1+λ2

∵λ∈[
2
2
，
2
]，
∴
1+λ2
∈[
6
2
，
3
]
∴sinθ∈[
1
2
，
2
2
]
∴θ∈[
π
6
，
π
4
]
故选B．
点评：本题考查线面角，考查向量知识的运用，考查学生的计算能力，确定线面角是关键．
练习册系列答案
相关题目
精英家教网如图，已知直三棱柱ABC-A1B1C1，∠ACB=90°，AC=BC=2，AA1=4．E、F分别是棱CC1、AB中点．
（Ⅰ）求证：CF⊥BB1；
（Ⅱ）求四棱锥A-ECBB1的体积；
（Ⅲ）判断直线CF和平面AEB1的位置关系，并加以证明．
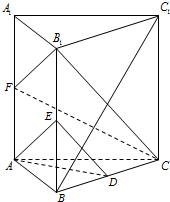已知直三棱柱ABC-A1B1C1的所有棱长都相等，且D，E，F分别为BC，BB1，AA1的中点．
（I） 求证：平面B1FC∥平面EAD；
（II）求证：BC1⊥平面EAD．
如图所示，已知直三棱柱ABC-A′B′C′，AC=AB=AA′=2，AC，AB，AA′两两垂直，E，F，H分别是AC，AB，BC的中点，
（I）证明：EF⊥AH；    
（II）求四面体E-FAH的体积．
如图，已知直三棱柱ABC-A1B1C1的侧棱长为2，底面△ABC是等腰直角三角形，且∠ACB=90°，AC=2，D是A A1的中点．
（Ⅰ）求异面直线AB和C1D所成的角（用反三角函数表示）；
（Ⅱ）若E为AB上一点，试确定点E在AB上的位置，使得A1E⊥C1D；
（Ⅲ）在（Ⅱ）的条件下，求点D到平面B1C1E的距离．
如图，已知直三棱柱ABC-A1B1C1中，AB=AC；M．N．P分别是棱BC．CC1．B1C1的中点．A1Q=3QA， BC=
2
AA1
（Ⅰ）求证：PQ∥平面ANB1；
（Ⅱ）求证：平面AMN⊥平面AMB1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网