题目内容
【题目】函数f（x）=4sinωxcos（ωx+ 
）+1（ω＞0），其图象上有两点A（s，t），B（s+2π，t），其中﹣2＜t＜2，线段AB与函数图象有五个交点． （Ⅰ）求ω的值；
（Ⅱ）若函数f（x）在[x1 ， x2]和[x3 ， x4]上单调递增，在[x2 ， x3]上单调递减，且满足等式x4﹣x3=x2﹣x1= 
（x3﹣x2），求x1、x4所有可能取值．
【答案】解：（Ⅰ）f（x）=4sinωxcos（ωx+ 
）+1=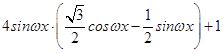 
= 
= 
= 
，
由于|AB|=2π，且线段AB与函数f（x）图象有五个交点，
因此 
，故ω=1；
（Ⅱ）由（Ⅰ）得，函数f（x）= ，由题意知 
，
因此x4﹣x3=x2﹣x1= 
（x3﹣x2）= 
．即 
， 
．
∵函数f（x）在[x1，x2]上单调递增，在[x2，x3]上单调递减，
∴f（x）在x2处取得最大值，即 
=2．
，即 
．
∴ = 
．
= 
．
【解析】（Ⅰ）利用三角函数的诱导公式化简即可得答案；（Ⅱ）求出函数f（x）的最值即可得答案．
练习册系列答案
相关题目
