题目内容
15.求函数f(x)=-x2+2x在[0,10]上的最大值和最小值.分析 先求出函数的对称轴,得到函数的单调区间,从而求出函数的最值.
解答 解:f(x)=-x2+2x-1+1=-(x-1)2+1,
对称轴x=1,
∴函数f(x)在[0,1)递增,在(1,10]递减,
∴f(x)最大值=1,f(x)最小值=f(10)=-80.
点评 本题考查了二次函数的性质,考查函数的单调性和最值问题,是一道基础题.

练习册系列答案
相关题目
20.将函数f(x)=$\sqrt{3}$sin2x-cos2x的图象向左平移|m|个单位,若所得的图象关于直线x=$\frac{π}{6}$对称,则|m|的最小值为( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | 0 | D. | $\frac{π}{12}$ |
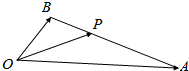 如图,在△ABC中,已知P为线段AB上一点,且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$.
如图,在△ABC中,已知P为线段AB上一点,且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$.