Question

17．已知函数g（x）=ax+1，f（x）=$\left\{\begin{array}{l}{{2}^{x}-1，0≤x≤2}\\{-{x}^{2}，-2≤x＜0}\end{array}\right.$  对?x₁∈[-2，2]，?x₂∈[-2，2]，使g（x₁）=f（x₂）成立，则实数a的取值范围是[-1，1]．

Answer 1

分析 作出函数f（x）的图象，根据条件求出两个函数最值之间的关系，结合数形结合即可得到结论．

解答 解：作出函数f（x）=$\left\{\begin{array}{l}{{2}^{x}-1，0≤x≤2}\\{-{x}^{2}，-2≤x＜0}\end{array}\right.$的图象如图：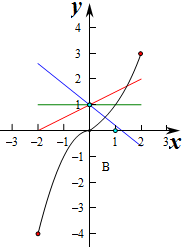
则当x∈[-2，2]，f（x）的最大值为f（2）=3，最小值f（-2）=-4，
若a=0，g（x）=1，此时满足?x₁∈[-2，2]，?x₂∈[-2，2]，
使g（x₁）=f（x₂）成立，
若a≠0，则直线g（x）过定点B（0，1），
若a＞0，要使对?x₁∈[-2，2]，?x₂∈[-2，2]，
使g（x₁）=f（x₂）成立，
则满足g（x）_max≤f（x）_max，且g（x）_min≥f（x）_min，
即2a+1≤3且-2a+1≥-4，
即a≤1且a≤$\frac{5}{2}$，
此时满足0＜a≤1，
若a＜0，要使对?x₁∈[-2，2]，?x₂∈[-2，2]，使g（x₁）=f（x₂）成立，
则满足g（x）_max≤f（x）_max，且g（x）_min≥f（x）_min，
即-2a+1≤3且2a+1≥-4，
即a≥-1且a≥-$\frac{5}{2}$，
此时满足-1≤a＜1，
综上-1≤a≤1，
故答案为：[-1，1]．

点评 本题主要考查函数与方程之间的关系，利用数形结合是解决本题的关键，本题主要考查的是最值之间的关系，综合性较强，有一定的难度．