题目内容
【题目】已知函数![]() .
.
(Ⅰ)若曲线![]() 在点
在点![]() 处的切线
处的切线![]() 与直线
与直线![]() 垂直,求
垂直,求![]() 的值;
的值;
(Ⅱ)若函数![]() 存在极值点
存在极值点![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:本题主要考查导数的运算、利用导数判断函数的单调性、利用导数求函数的极值等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,先对![]() 求导,将
求导,将![]() 代入
代入![]() 中,即得到切线的斜率,而两直线垂直,则两个斜率相乘为-1,解出a的值;第二问,先对
中,即得到切线的斜率,而两直线垂直,则两个斜率相乘为-1,解出a的值;第二问,先对![]() 求导,由于导数中有参数a,则讨论
求导,由于导数中有参数a,则讨论![]() 和
和![]() 两种情况,由于
两种情况,由于![]() 的解集为增区间,
的解集为增区间, ![]() 的解集为减区间,计算单调区间,利用函数的单调性判断极值点的位置,令极值点的横坐标在
的解集为减区间,计算单调区间,利用函数的单调性判断极值点的位置,令极值点的横坐标在![]() 之间,解不等式,解出a的取值范围.
之间,解不等式,解出a的取值范围.
试题解析:(Ⅰ)由于![]() , (2分)
, (2分)
又![]()
![]() . (4分)
. (4分)
(Ⅱ)![]() ,
,
①当![]() 时,
时, ![]() ,函数
,函数![]() 在
在![]() 上单调递增,无极值; (6分)
上单调递增,无极值; (6分)
②当![]() 时,令
时,令![]() 即
即![]() ,
,
![]() ,
,
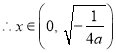 时,函数
时,函数![]() 单调递增;
单调递增;  时,函数
时,函数![]() 单调递减, (8分)
单调递减, (8分)
故![]() 是
是![]() 的极大值点.依题意:
的极大值点.依题意: ![]() , (10分)
, (10分)
解得: ![]() ,综上所述,
,综上所述, ![]() 的取值范围为
的取值范围为![]() . (12分)
. (12分)

【题目】随机抽取一个年份,对西安市该年4月份的天气情况进行统计,结果如下:
(1)在4月份任取一天,估计西安市在该天不下雨的概率;
(2)西安市某学校拟从4月份的一个晴天开始举行连续2天的运动会,估计运动会期间不下雨的概率.
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
天气 | 晴 | 雨 | 阴 | 阴 | 阴 | 雨 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 晴 |
日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
天气 | 晴 | 阴 | 雨 | 阴 | 阴 | 晴 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 雨 |
【题目】某海滨浴场每年夏季每天的海浪高度y(米)是时间x(0≤x≤24,单位:小时)的函数,记作y=f(x),下表是每年夏季每天某些时刻的浪高数据:
x(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y(米) | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 |
(1)经观察发现可以用三角函数y=Acosωx+b对这些数据进行拟合,求函数f(x)的表达式;
(2)浴场规定,每天白天当海浪高度高于1.25米时,才对冲浪爱好者开放,求冲浪者每天白天可以在哪个时段到该浴场进行冲浪运动?
【题目】通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
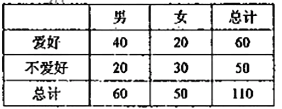
由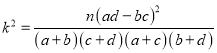 算得,
算得, ![]() .
.
P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
则参照附表,得到的正确结论应是( )
A. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
C. 有99%以上的把握认为“爱好该项运动与性别有关”
D. 有99%以上的把握认为“爱好该项运动与性别无关”