题目内容
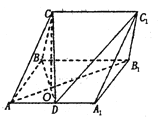
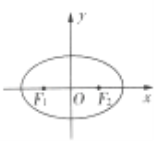
【题目】平面直角坐标系xOy中,已知F1、F2分别是椭圆C:![]() +
+![]() =1(a>b>0)的左、右焦点,且右焦点F2的坐标为(
=1(a>b>0)的左、右焦点,且右焦点F2的坐标为(![]() ,0),点(
,0),点(![]() ,
,![]() )在椭圆C上.
)在椭圆C上.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)在椭圆C上任取一点P,点Q在PO的延长线上,且![]() =2.
=2.
(1)当点P在椭圆C上运动时,求点Q形成的轨迹E的方程;
(2)若过点P的直线l:y=x+m交(1)中的曲线E于A,B两点,求△ABQ面积的最大值.
【答案】(I)![]() ;(II)(1)
;(II)(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(Ⅰ)利用椭圆的焦点坐标和点在椭圆![]() 上,列出方程组,求出
上,列出方程组,求出![]() ,由此能求出椭圆的标准方程;(Ⅱ)(1)设
,由此能求出椭圆的标准方程;(Ⅱ)(1)设![]() ,则
,则![]() ,由此能求出当点
,由此能求出当点![]() 在椭圆
在椭圆![]() 上运动时,求点
上运动时,求点![]() 形成的轨迹
形成的轨迹![]() 的方程;(2)联立
的方程;(2)联立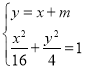 ,得
,得![]() ,由此利用根的判别式、韦达定理、弦长公式、点到直线距离公式,结合已知能求出
,由此利用根的判别式、韦达定理、弦长公式、点到直线距离公式,结合已知能求出![]() 面积的最大值.
面积的最大值.
试题解析:
(Ⅰ)∵F1、F2分别是椭圆C:![]() +
+![]() =1(a>b>0)的左、右焦点,
=1(a>b>0)的左、右焦点,
且右焦点F2的坐标为(![]() ,0),点(
,0),点(![]() ,
,![]() )在椭圆C上,
)在椭圆C上,
∴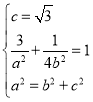 ,解得a=2,b=1,
,解得a=2,b=1,
∴椭圆C的标准方程为![]() +y2=1.
+y2=1.
(Ⅱ)(1)∵在椭圆C上任取一点P,点Q在PO的延长线上,且![]() =2,
=2,
∴设P(2cosθ,sinθ),则Q(4cosθ,2sinθ),0≤θ<2π,
∴当点P在椭圆C上运动时,求点Q形成的轨迹E的方程:
![]() ,0≤θ<2π,
,0≤θ<2π,
∴点E的直角坐标方程为:![]() =1.
=1.
(2)联立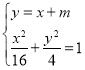 ,得5x2+8mx+4m2﹣16=0,
,得5x2+8mx+4m2﹣16=0,
设A(x1,y1),B(x2,y2),则![]() ,
,![]() ,
,
△=64m2﹣80m2+320>0,解得﹣2![]() ,
,
|AB|=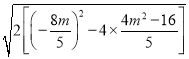 =
=![]() ,
,
设Q(4cosθ,2sinθ),则Q到直线y=x+m的距离d=![]() =
=![]() |2
|2![]() sin(θ+α)+m|,
sin(θ+α)+m|,
∴当m=0时,△ABQ面积取最大值S=![]() =8.
=8.

练习册系列答案
相关题目