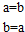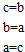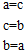题目内容
15.在[-2,2]上作函数y=2|x+1|+|x|+|x-1|的图象,并解不等式y=2|x+1|+|x|+|x-1|>5.分析 利用已知条件化简函数的解析式,然后画出函数的图象,借助函数的图象求解不等式的解集即可.
解答 解:函数y=2|x+1|+|x|+|x-1|=$\left\{\begin{array}{l}-4x-1,x∈[-2,-1]\\ 3,x∈(-1,0]\\ 2x+3,x∈(0,1]\\ 4x+1,x∈(1,2]\end{array}\right.$,
函数的图象如图: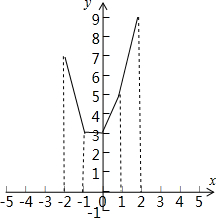
2|x+1|+|x|+|x-1|>5.
由函数的图象可得:x>1或$\left\{\begin{array}{l}x<-1\\-4x-1>5\end{array}\right.$,
解得x>1或x$<-\frac{3}{2}$.
点评 本题考查函数的解析式的化简,函数的图象的作法,绝对值不等式的解法,考查计算能力.

练习册系列答案
相关题目
3.已知z1,z2是复数,下列结论错误的是( )
| A. | 若|z1-z2|=0,则$\overline{{z}_{1}}$=$\overline{{z}_{2}}$ | B. | 若 z1=$\overline{{z}_{2}}$,则$\overline{{z}_{1}}$=z2 | ||
| C. | 若|z1|=|z2|,则z1•$\overline{{z}_{1}}$=z2$\overline{{z}_{2}}$ | D. | 若|z1|=|z2|,则z12=z22 |
7.已知A={x|1≤x≤5},B={x|(x-a+1)(x-a-1)≤0},条件p:x∈A,条件q:x∈B,若?p是?q的充分不必要条件,则实数a的取值范围是( )
| A. | (2,4] | B. | [2,4] | C. | [2,4) | D. | (2,4) |