题目内容
设函数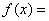
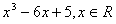 .
.
(1)求函数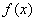 的单调区间和极值。
的单调区间和极值。
(2)若关于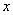 的方程
的方程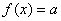 有三个不同实根,求实数
有三个不同实根,求实数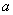 的取值范围;
的取值范围;
(3)已知当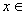 (1,+∞)时,
(1,+∞)时,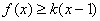 恒成立,求实数
恒成立,求实数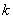 的取值范围.
的取值范围.
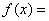
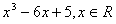 .
.(1)求函数
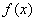 的单调区间和极值。
的单调区间和极值。(2)若关于
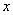 的方程
的方程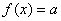 有三个不同实根,求实数
有三个不同实根,求实数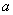 的取值范围;
的取值范围;(3)已知当
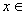 (1,+∞)时,
(1,+∞)时,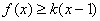 恒成立,求实数
恒成立,求实数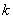 的取值范围.
的取值范围.(1)f(x)的单调递增区间为(-∞,- )和(
)和( ,+∞);单调减区间为(-
,+∞);单调减区间为(- ,
, ).当x=-
).当x=- 时,f(x)有极大值5+4
时,f(x)有极大值5+4 ;当x=
;当x= 时,f(x)有极小值5-4
时,f(x)有极小值5-4 .
.
(2)-4 <a<5+4
<a<5+4
(3)k≤-3
 )和(
)和( ,+∞);单调减区间为(-
,+∞);单调减区间为(- ,
, ).当x=-
).当x=- 时,f(x)有极大值5+4
时,f(x)有极大值5+4 ;当x=
;当x= 时,f(x)有极小值5-4
时,f(x)有极小值5-4 .
. (2)-4
 <a<5+4
<a<5+4
(3)k≤-3
试题分析:(1) 解:f′(x)=3x2-6,令f′(x)=0,解得x1=-
 ,x2=
,x2= .
.因为当x>
 或x<-
或x<- 时,f′(x)>0;当-
时,f′(x)>0;当- <x<
<x< 时,f′(x)<0.
时,f′(x)<0.所以f(x)的单调递增区间为(-∞,-
 )和(
)和( ,+∞);单调减区间为(-
,+∞);单调减区间为(- ,
, ).
).当x=-
 时,f(x)有极大值5+4
时,f(x)有极大值5+4 ;
;当x=
 时,f(x)有极小值5-4
时,f(x)有极小值5-4 . ---————-3分
. ---————-3分(2)由(1)的分析知 y=f(x)的图象的大致形状及走向如图所示,当5-4
 <a<5+4
<a<5+4 时,直线y=a与y=f(x)的图象有三个不同交点,即方程f(x)=a有三个不同的
时,直线y=a与y=f(x)的图象有三个不同交点,即方程f(x)=a有三个不同的 6分
6分(3) 解:f(x)≥k(x-1),即(x-1)(x2+x-5)≥k(x-1).
因为x>1,所以k≤x2+x-5在(1,+∞)上恒成立.
令g(x)=x2+x-5,此函数在(1,+∞)上是增函数.
所以g(x)>g(1)=-3.
所以k的取值范围是k≤-3. 10分
点评:本题考查了利用导数求函数单调区间和极值的方法,利用导数研究函数图象解决根的个数问题的方法,不等式恒成立问题的解法

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
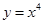 的一条切线
的一条切线 与直线
与直线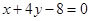 垂直,则
垂直,则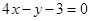
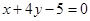
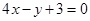
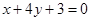
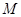 为曲线
为曲线 上的任意一点,在点
上的任意一点,在点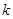 ,则
,则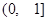 B
B C.
C.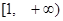 D.
D.
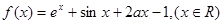
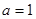 ,求曲线
,求曲线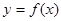 在
在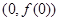 处的切线方程;
处的切线方程;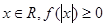 恒成立,求
恒成立,求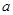 的取值范围。
的取值范围。 轴上一点A分别向函数
轴上一点A分别向函数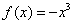 与函数
与函数 引不是水平方向的切线
引不是水平方向的切线 和
和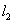 ,两切线
,两切线 轴相交于点B和点C,O为坐标原点,记△OAB的面积为
轴相交于点B和点C,O为坐标原点,记△OAB的面积为 ,△OAC的面积为
,△OAC的面积为 ,则
,则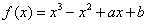 在点
在点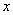 =1处的切线与直线
=1处的切线与直线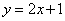 垂直,
垂直,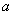 =________.
=________.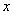 ,有
,有 ,且
,且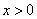 时,
时,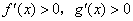 ,则
,则 时
时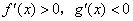
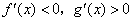
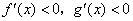
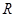 上的函数
上的函数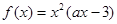 ,其中
,其中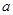 为常数.
为常数.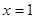 是函数
是函数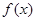 的一个极值点,求
的一个极值点,求 上是增函数,求
上是增函数,求