Question

某校高二年级共有学生1000名，其中走读生750名，住宿生250名，现从该年级采用分层抽样的方法从该年级抽取n名学生进行问卷调查．根据问卷取得了这n名同学每天晚上有效学习时间（单位：分钟）的数据，按照以下区间分为八组：
①[0，30），②[30，60），③[60，90），④[90，120），
⑤[120，150），⑥[150，180），⑦[180，210），⑧[210，240），
得到频率分布直方图如下．已知抽取的学生中每天晚上有效学习时间少于60分钟的人数为5人；
（1）求n的值并补全下列频率分布直方图；
（2）如果把“学生晚上有效时间达到两小时”作为是否充分利用时间的标准，对抽取的n名学生，完成下列2×2列联表：

	利用时间充分	利用时间不充分	总计
走读生	50	25	75
住宿生	10	15	25
总计	60	40	100

是否有95%的把握认为学生利用时间是否充分与走读、住宿有关？
参考公式：K2=

n(ad-bc)2

(a+b)(c+d)(a+c)(b+d)

参考列表：

P（K2≥k0）	0.50	0.40	0.25	0.15	0.10	0.05	0.025
k0	0.455	0.708	1.323	2.072	2.706	3.841	5.024

（3）若在第①组、第②组、第⑦组、第⑧组中共抽出3人调查影响有效利用时间的原因，记抽到“有效学习时间少于60分钟”的学生人数为X，求X的分布列及期望．

Answer 1

分析：（1）设第i组的频率为P_i（i=1，2，…，8），则由图可知：学习时间少于60钟的频率为：P₁+P₂=

5

100

，由此能够求出n的值并补全频率分布直方图．
（2）求出K²，比较K²与3.841的大小，能够判断是否有95%的把握认为学生利用时间是否充分与走读、住宿有关．
（3）由题设条X的所有可能取值为0，1，2，3，分别求出其概率，能够得到X的分布列和EX．

解答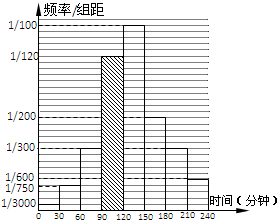：解：（1）设第i组的频率为P_i（i=1，2，…，8），
则由图可知：P₁=

1

3000

×30=

1

100

，P₂=

1

750

×30=

4

100

，
∴学习时间少于60钟的频率为：P₁+P₂=

5

100

，
由题n×

5

100

=5∴n=100，…（2分）
又P₃=

1

300

×30=

10

100

，P₅=

1

100

×30=

30

100

，
P₆=

1

200

×30=

15

100

，P₇=

1

300

×30=

10

100

，
P₈=

1

600

×30=

5

100

，
∴P₄=1-（P₁+P₂+P₃+P₅+P₆+P₇+P₈）
=1-

1+4+10+30+15+10+5

100

=1-

75

100

=

25

100

，
第④组的高度h=

25

100

×

1

30

=

25

3000

=

1

120

．
频率分布直方图如图：（未标明高度1/120扣1分）…（4分）
（2）K²=

100×(50×15-25×10)2

75×25×40×60

≈5.556
由于K²＞3.841，
所以有95%的把握认为学生利用时间是否充分与走读、住宿有关…（8分）
（3）由（1）知：第①组1人，
第②组4人，第⑦组15人，第⑧组10人，总计20人．
则X的所有可能取值为0，1，2，3，
P（X=i）=

C i 5 C 3-i 15

C 3 20

，（i=0，1，2，3），
∴P（X=0）=

C 0 5 C 3 15

C 3 20

=

91

228

，
P（X=1）=

C 1 5 C 2 15

C 3 20

=

35

76

，
P（X=2）=

C 2 5 C 1 15

C 3 20

=

30

228

，
P（X=3）=

C 3 5 C 0 15

C 3 20

=

1

114

，
∴X的分布列为：

P	0	1	2	3
X	91 228	35 76	5 38	1 114

EX=0×

91

228

+1×

105

228

+2×

30

228

+3×

2

228

=

1×105+2×30+3×2

228

=

171

228

=

3

4

．

点评：本题考查离散型随机变量的分布列和数学期望，是中档题，在历年高考中都是必考题型．解题时要认真审题，仔细解答，注意排列组合和概率知识的灵活运用．