题目内容
8.已知集合A={x|x2-4x-21=0},B={x|5x-a≥3x+2,a∈R}.(1)用列举法表示集合A;
(2)若A∪B=B,求实数a的取值范围.
分析 (1)解方程x2-4x-21=0,用列举法表示即可,
(2)先化简,再根据A∪B=B得到A⊆B,得到a的取值范围.
解答 解:(1)A={x|x2-4x-21=0}={-3,7}
(2)B={x|5x-a≥3x+2,a∈R}={x|x≥$\frac{a+2}{2}$},
∵A∪B=B,
∴A⊆B,
∴$\frac{a+2}{2}$≤3,
解得a≤-8,
故数a的取值范围为(-∞,-8].
点评 本题考查了交集并集及其运算,熟练掌握交集并集的定义是解本题的关键.

练习册系列答案
相关题目
16.已知集合A={x|x>0},B={x|-1<x<5}则A∩B=( )
| A. | {x|x>-1} | B. | {x|-1<x<5} | C. | {x|0<x<5} | D. | {x|x<5} |
3.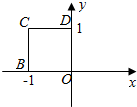 已知函数f(x)=$|\begin{array}{l}{x}\end{array}|,x∈[a,b]$值域是[0,1],那么点p(a,b) 在平面角坐标系中的位置位于图中的( )
已知函数f(x)=$|\begin{array}{l}{x}\end{array}|,x∈[a,b]$值域是[0,1],那么点p(a,b) 在平面角坐标系中的位置位于图中的( )
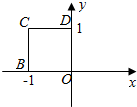 已知函数f(x)=$|\begin{array}{l}{x}\end{array}|,x∈[a,b]$值域是[0,1],那么点p(a,b) 在平面角坐标系中的位置位于图中的( )
已知函数f(x)=$|\begin{array}{l}{x}\end{array}|,x∈[a,b]$值域是[0,1],那么点p(a,b) 在平面角坐标系中的位置位于图中的( )| A. | 线段OB和OD | B. | 线段BC和CD | C. | 线段BC和BO | D. | 线段OB和CD |
13.对于命题p、q,其中p:对于任意的x∈R,不等式ax2+x+1<0解集为空集;命题q:f(x)=(5a-4)x在R上为减函数,如果命题p∧¬q为真命题,那么实数a的取值范围是( )
| A. | (-∞,-1) | B. | (-1,0) | C. | (0,1) | D. | [$\frac{1}{4}$,$\frac{4}{5}$]∪[1,+∞) |
20.已知f(x)是定义在(0,+∞)上的单调递减函数,f′(x)是其导函数,若 $\frac{f(x)}{f′(x)}$>x,则下列不等关系成立的是( )
| A. | f(2)<2f(1) | B. | 3f(2)>2f(3) | C. | ef(e)<f(e2) | D. | ef(e2)>f(e3) |
18.已知复数z=-$\sqrt{3}$+3i,则z在复平面所对应的坐标是( )
| A. | (3,$\sqrt{3}$) | B. | ($\sqrt{3}$,3) | C. | (3,-$\sqrt{3}$) | D. | (-$\sqrt{3}$,3) |