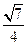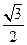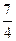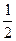题目内容
(本题满分15分)已知椭圆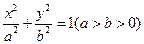 的离心率为
的离心率为 ,椭圆上任意一点到右焦点
,椭圆上任意一点到右焦点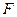 的距离的最大值为
的距离的最大值为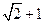 。
。
(I)求椭圆的方程;
(II)已知点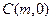 是
是 线段
线段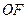 上一个动点(
上一个动点(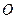
 为坐标原点),是否存在过点
为坐标原点),是否存在过点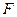 且与
且与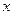 轴不垂直的直线
轴不垂直的直线 与椭圆交于
与椭圆交于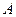 、
、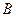 两点,使得
两点,使得 ,并说明理由。
,并说明理由。
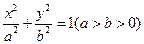 的离心率为
的离心率为 ,椭圆上任意一点到右焦点
,椭圆上任意一点到右焦点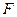 的距离的最大值为
的距离的最大值为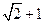 。
。(I)求椭圆的方程;
(II)已知点
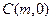 是
是 线段
线段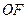 上一个动点(
上一个动点(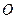
 为坐标原点),是否存在过点
为坐标原点),是否存在过点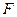 且与
且与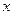 轴不垂直的直线
轴不垂直的直线 与椭圆交于
与椭圆交于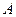 、
、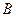 两点,使得
两点,使得 ,并说明理由。
,并说明理由。(I)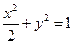 ;
;
(II)当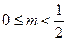 时,
时,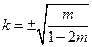 ,即存在这样的直线
,即存在这样的直线 ;
;
当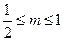 ,
,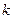 不存在,即不存在这样的直线
不存在,即不存在这样的直线
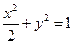 ;
;(II)当
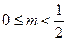 时,
时,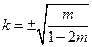 ,即存在这样的直线
,即存在这样的直线 ;
;当
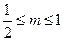 ,
,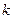 不存在,即不存在这样的直线
不存在,即不存在这样的直线
(1)因为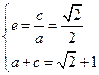 , 所以
, 所以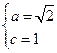 , …………(4分)
, …………(4分)
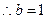 ,椭圆方程为:
,椭圆方程为: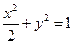 …………(6分)
…………(6分)
(2)由(1)得 ,所以
,所以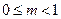 ,假设存在满足题意的直线
,假设存在满足题意的直线 ,
, 设
设 的方程为
的方程为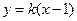 ,代入
,代入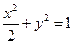 ,得
,得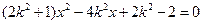
设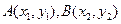 ,则
,则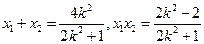 ①, …………(10分)
①, …………(10分)
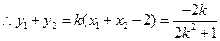
设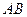 的中点为
的中点为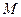 ,则
,则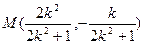 ,
,
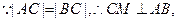 即
即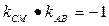
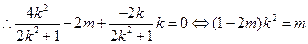
 当
当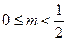 时,
时,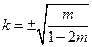 ,即存在这样的直线
,即存在这样的直线 ;
;
当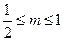 ,
,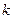 不存在,即不存在这样的直线
不存在,即不存在这样的直线 …………(15分)
…………(15分)
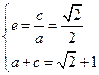 , 所以
, 所以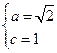 , …………(4分)
, …………(4分)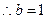 ,椭圆方程为:
,椭圆方程为: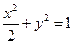 …………(6分)
…………(6分)(2)由(1)得
 ,所以
,所以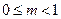 ,假设存在满足题意的直线
,假设存在满足题意的直线 ,
, 设
设 的方程为
的方程为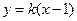 ,代入
,代入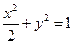 ,得
,得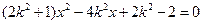
设
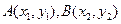 ,则
,则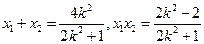 ①, …………(10分)
①, …………(10分)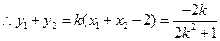
设
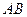 的中点为
的中点为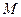 ,则
,则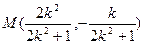 ,
,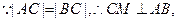 即
即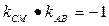
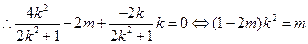
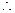 当
当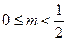 时,
时,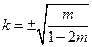 ,即存在这样的直线
,即存在这样的直线 ;
;当
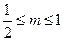 ,
,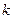 不存在,即不存在这样的直线
不存在,即不存在这样的直线 …………(15分)
…………(15分)
练习册系列答案
相关题目
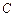 :
: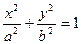 (a>b>0)的中心在原点,焦点在
(a>b>0)的中心在原点,焦点在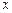 轴上,离心率为
轴上,离心率为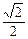 ,点F1、F2分别是椭圆的左、右焦点,在直线x=2上的点P(2,
,点F1、F2分别是椭圆的左、右焦点,在直线x=2上的点P(2, 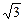 )满足|PF2|=|F1F2|,直线l:y=kx+m与椭圆C交于不同的两点A、 B.
)满足|PF2|=|F1F2|,直线l:y=kx+m与椭圆C交于不同的两点A、 B.
 存在点Q,满足
存在点Q,满足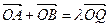 (O为坐标原点),求实数l的取值范围.
(O为坐标原点),求实数l的取值范围.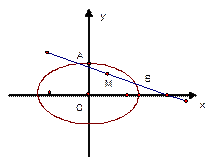
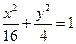 内一点M(1,1)的弦AB
内一点M(1,1)的弦AB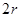 ,短半轴长为
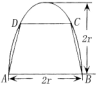
,短半轴长为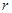 ,计划将此钢板切割成等腰梯形的形状,下底
,计划将此钢板切割成等腰梯形的形状,下底 是半椭圆的短轴,上底
是半椭圆的短轴,上底 的端点在椭圆上,记
的端点在椭圆上,记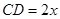 ,梯形面积为
,梯形面积为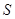 .
.
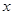 为自变量的函数式,并写出其定义域;
为自变量的函数式,并写出其定义域;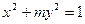 的焦点在
的焦点在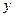 轴上,长轴长是短轴长的两倍,则
轴上,长轴长是短轴长的两倍,则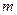 的值为( )
的值为( )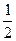
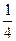
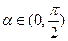 ,方程
,方程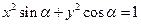 表示焦点在
表示焦点在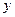 轴上的椭圆,则
轴上的椭圆,则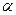 的取值范围是()
的取值范围是()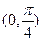
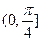
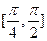
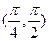
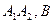 为短轴一端点,若
为短轴一端点,若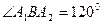 ,则椭圆的离心率为( )
,则椭圆的离心率为( )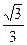
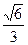
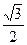
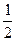
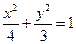 的离心率为
的离心率为