Question

（2009•杨浦区一模）如图，过圆锥轴的截面为等腰直角三角形SAB，Q为底面圆周上一点，已知BQ=2

3

，圆锥体积为

8

3

π，点O为底面圆的圆心．
（1）．求该圆锥的侧面积；
（2）．设异面直线SA与BQ所成角的大小为θ，求tanθ的值．

Answer 1

分析：（1）设底面圆的半径为R，则高R=SO，利用体积公式求出R，再求出侧面积．
（2）连接QO并延长交圆周于C点，再连接AC，AQ，BC，SC，则AO=BO=QO=OC，所以 四边形AQBC是平行四边形，AC∥QB，∠SAC的大小为异面直线SA与BQ所成角θ的大小．

解答：解（1）设底面圆的半径为R，则由题意得R=SO，----（1分）
∵

1

3

πR2R=

8

3

π，∴R=2----------------（3分）
母线的长为SA=

R2+R2

=2

2

，-------------（4分）
所以，圆锥的侧面积为πR•SA=4

2

π-------------（6分）
（2）连接QO并延长交圆周于C点，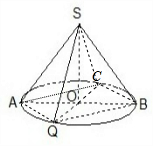
 再连接AC，AQ，BC，SC，------（7分）
则AO=BO=QO=OC，所以 四边形AQBC是平行四边形，AC∥QB，
∠SAC的大小为异面直线SA与BQ所成角θ的大小-----（10分）
由（1）知，在△SAC中，SA=SC=2

2

，AC=QB=2

3

，------------------（11分）
过点S作SH⊥AC于点H，
则tanθ=

SH

AH

=

SA2-AH2

AH

=

5

3

=

15

3

，∴θ=arctan

15

3

---------------（14分）

点评：本题主要考查空间角，圆锥体积，侧面积计算，考查了空间想象能力、计算能力，分析解决问题能力．空间问题平面化是解决空间几何体问题最主要的思想方法．