题目内容
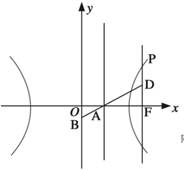 如图,已知双曲线
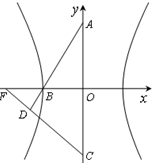
如图,已知双曲线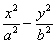 (a>0,b>0)其右准线交x轴于点A,双曲线虚轴的下端点为B,过双曲线的右焦点F(c,0)作垂直于x轴的直线交双曲线于点P,若点D满足:
(a>0,b>0)其右准线交x轴于点A,双曲线虚轴的下端点为B,过双曲线的右焦点F(c,0)作垂直于x轴的直线交双曲线于点P,若点D满足: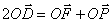 (O为原点)且
(O为原点)且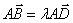 (λ≠0)
(λ≠0)
(Ⅰ)求双曲线的离心率;
(Ⅱ)若a=2,过点B的直线l交双曲线于M、N两点,
若存在,求出C点的坐标,若不存在,请说明理由.
练习册系列答案
相关题目
 如图,已知双曲线x2-
如图,已知双曲线x2-| y2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
题目内容
 如图,已知双曲线
如图,已知双曲线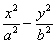 (a>0,b>0)其右准线交x轴于点A,双曲线虚轴的下端点为B,过双曲线的右焦点F(c,0)作垂直于x轴的直线交双曲线于点P,若点D满足:
(a>0,b>0)其右准线交x轴于点A,双曲线虚轴的下端点为B,过双曲线的右焦点F(c,0)作垂直于x轴的直线交双曲线于点P,若点D满足: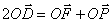 (O为原点)且
(O为原点)且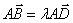 (λ≠0)
(λ≠0)
(Ⅰ)求双曲线的离心率;
(Ⅱ)若a=2,过点B的直线l交双曲线于M、N两点,
若存在,求出C点的坐标,若不存在,请说明理由.
 如图,已知双曲线x2-
如图,已知双曲线x2-| y2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|