题目内容
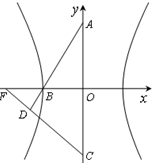如图，已知双曲线x2-| y2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析：利用双曲线的简单性质求出直线方程，求出三角形三个顶点的坐标，利用余弦定理求得cos∠BDF 的值．
解答：解：由题意得A（0，b），C（0，-b），B（-a，0），F（-c，0），
=2．
∴BF=c-a=a，BD 的方程为
+
=1，即 bx-ay+ab=0，
DC的方程为
+
=1，即 bx+cy+bc=0，即 bx+2ay+2ab=0，
由
得 D （-
，-
），又 b=
=
a，
∴FD=
=
，BD=
=
，
三角形BDF中，由余弦定理得 a2=
a2+
a2-2
•
cos∠BDF，
∴cos∠BDF=
，
故选 C．
| c |
| a |
∴BF=c-a=a，BD 的方程为
| x |
| -a |
| y |
| b |
DC的方程为
| x |
| -c |
| y |
| -b |
由
|
| 4a |
| 3 |
| b |
| 3 |
| c2- a2 |
| 3 |
∴FD=
(-c+
|
|
(-a+
|
|
三角形BDF中，由余弦定理得 a2=
| 7 |
| 9 |
| 4 |
| 9 |
|
|
∴cos∠BDF=
| ||
| 14 |
故选 C．
点评：本题考查求直线方程，求两直线的焦点坐标，余弦定理，以及双曲线的简单性质的应用．
练习册系列答案
阅读快车系列答案
相关题目
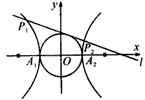
（2013•上海）如图，已知双曲线C1：
，曲线C2：|y|=|x|+1，P是平面内一点，若存在过点P的直线与C1，C2都有公共点，则称P为“C1﹣C2型点“
内的点都不是“C1﹣C2型点”