题目内容
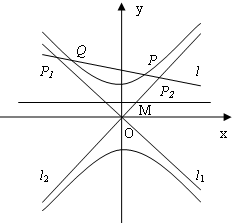 如图,已知双曲线C:
如图,已知双曲线C:| y2 |
| a2 |
| x2 |
| b2 |
| 2 |
| MF1 |
| MF2 |
(1)求双曲线C的方程;
(2)直线l交双曲线C的渐近线l1、l2于P1、P2,交双曲线于P、Q,且
| P1P |
| PP2 |
| PQ |
分析:(1)设出焦点坐标,利用
•
=-1,结合离心率,求出a,c,b,即可求双曲线C的方程;
(2)设出直线l的方程,求出直线交双曲线C的渐近线l1、l2于P1、P2,结合
=2
,通过P在双曲线上,通过弦长公式求|
|的最小值.
| MF1 |
| MF2 |
(2)设出直线l的方程,求出直线交双曲线C的渐近线l1、l2于P1、P2,结合
| P1P |
| PP2 |
| PQ |
解答:解:(1)设F1(0,c),F2(0,c)则M(
,
),由
•
=-1,
得(
)2-(c-
)(c+
)=a2-c2=-1;
∵e=
=
,
∴a=1,c=
,
所以双曲线C的方程为:y2-x2=1.…(6分)
(2)设直线l的方程为y=kx+b,交双曲线C的渐近线l1、l2于P1(-
,
),P2(
,
);
由
=2
可得P(
,
)
因为P在双曲线上,所以(
)2-(
)2=1,
所以8b2=9(1-k2),
联立得
即(k2-1)x2+2kbx+b2-1=0…(10分)
∴|
|=
=
≥
.
当且仅当k=0时取等号.
| ab |
| c |
| a2 |
| c |
| MF1 |
| MF2 |
得(
| ab |
| c |
| a2 |
| c |
| a2 |
| c |
∵e=
| c |
| a |
| 2 |
∴a=1,c=
| 2 |
所以双曲线C的方程为:y2-x2=1.…(6分)
(2)设直线l的方程为y=kx+b,交双曲线C的渐近线l1、l2于P1(-
| b |
| 1+k |
| b |
| 1+k |
| b |
| 1+k |
| b |
| 1+k |
由
| P1P |
| PP2 |
| 3kb+b |
| 3(1-k2) |
| 3b+bk |
| 3(1-k2) |
因为P在双曲线上,所以(
| 3kb+b |
| 3(1-k2) |
| 3b+bk |
| 3(1-k2) |
所以8b2=9(1-k2),
联立得
|
∴|
| PQ |
| (1+k2)[(x1+x2)2-4 x1x2] |
| ||
|
| ||
| 2 |
当且仅当k=0时取等号.
点评:此题是难题.考查双曲线的定义和简单的几何性质,以及直线和椭圆相交中的有关中点弦的问题,综合性强,特别是问题(2)的设问形式,增加了题目的难度,注意直线与圆锥曲线相交弦长的求法.体现了数形结合和转化的思想方法.

练习册系列答案
相关题目
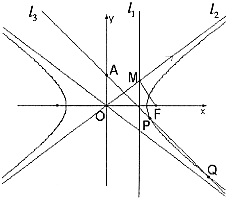 如图,已知双曲线C:
如图,已知双曲线C: 如图,已知双曲线C:
如图,已知双曲线C: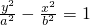 (a>0,b>0)的离心率e=
(a>0,b>0)的离心率e= ,F1、F2分别为双曲线C的上、下焦点,M为上准线与渐近线在第一象限的交点,且
,F1、F2分别为双曲线C的上、下焦点,M为上准线与渐近线在第一象限的交点,且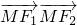 =-1.
=-1.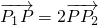 ,求|
,求| |的最小值.
|的最小值. (a>0,b>0)的离心率e=
(a>0,b>0)的离心率e= ,F1、F2分别为双曲线C的上、下焦点,M为上准线与渐近线在第一象限的交点,且
,F1、F2分别为双曲线C的上、下焦点,M为上准线与渐近线在第一象限的交点,且 =-1.
=-1.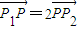 ,求|
,求| |的最小值.
|的最小值.
 (a>0,b>0)的离心率e=
(a>0,b>0)的离心率e=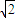 ,F1、F2分别为双曲线C的上、下焦点,M为上准线与渐近线在第一象限的交点,且
,F1、F2分别为双曲线C的上、下焦点,M为上准线与渐近线在第一象限的交点,且 =-1.
=-1.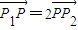 ,求|
,求| |的最小值.
|的最小值.