题目内容
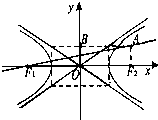 如图,已知双曲线E:
如图,已知双曲线E:| x2 |
| a2 |
| y2 |
| b2 |
F1(-c,0)、F2(c,0),点A(c,b),B(0,b),O为坐标原点,直线OA与直线F2B的交点在双曲线E上.
(1)求双曲线E的离心率;
(2)设直线F1A与双曲线E 交于M、N两点,
| F1M |
| MA |
| F1N |
| NA |
(3)在(2)的条件下,过点B的直线与双曲线E相交于不同的两点P、Q,求
| BP |
| BQ |
分析:(1)将F2B的中点(
,
)代入双曲线E的方程可得
-
=1,由此能导出e.
(2)由e=
得a2=
b2,化简方程E为4x2-y2=b2,又直线F1A的方程为y=
(x+c),代入双曲线E化简得(20b2-1)y2-20by+4b2=0,由此能得到所求双曲线E的方程.
(3)由B(0,1),设直线BP的方程为y=kx+1,代入双曲线E的方程4x2-y2=1,得(4-k2)x2-2kx-2=0,记P(x1,y1),Q(x2,y2),则
,由此能得到
•
的取值范围.
| c |
| 2 |
| b |
| 2 |
| c2 |
| 4a2 |
| 1 |
| 4 |
(2)由e=
| 5 |
| 1 |
| 2 |
| b |
| 2c |
(3)由B(0,1),设直线BP的方程为y=kx+1,代入双曲线E的方程4x2-y2=1,得(4-k2)x2-2kx-2=0,记P(x1,y1),Q(x2,y2),则
|
| BP |
| BQ |
解答:解:(1)将F2B的中点(
,
)代入双曲线E的方程可得:
-
=1
则e=
.
(2)由e=
得a2=
b2,化简方程E为:
4x2-y2=b2
又直线F1A的方程为y=
(x+c),即x=c(
-1),
代入双曲线E化简得:
(20b2-1)y2-20by+4b2=0,
设M(x1,y1),N(x2,y2)
∴
由题意知,λ=
=
,μ=
=
,
则λ+μ=
+
=
=
=4,
∴b2=1,
即b=1
故所求双曲线E的方程为4x2-y2=1
(3)由(2)知B(0,1),由题意可设直线BP的方程为:
y=kx+1
代入双曲线E的方程4x2-y2=1,化简得:
(4-k2)x2-2kx-2=0,
记P(x1,y1),Q(x2,y2),
则
∴k2<8
•
=(x1,y1-1) •(x2,y2-2)=
,
令
•
=m,则k2=
∵0≤k2≤8
∴0≤
<8,
解得m≤-
或m>
,
故所求
•
的取值范围为(-∞,-
]∪(
,+∞)∪(
,+∞).
| c |
| 2 |
| b |
| 2 |
| c2 |
| 4a2 |
| 1 |
| 4 |
则e=
| 5 |
(2)由e=
| 5 |
| 1 |
| 2 |
4x2-y2=b2
又直线F1A的方程为y=
| b |
| 2c |
| 2y |
| b |
代入双曲线E化简得:
(20b2-1)y2-20by+4b2=0,
设M(x1,y1),N(x2,y2)
∴
|
由题意知,λ=
| |F 1M| |
| |MA| |
| y1 |
| b-y1 |
| |F1N| |
| |NA| |
| y2 |
| b-y2 |
则λ+μ=
| y1 |
| b-y1 |
| y2 |
| b-y2 |
| b(y1+y2)-2y1y2 |
| b2-b(y1+y2)+y1y2 |
| 12 |
| 20b2-17 |
∴b2=1,
即b=1
故所求双曲线E的方程为4x2-y2=1
(3)由(2)知B(0,1),由题意可设直线BP的方程为:
y=kx+1
代入双曲线E的方程4x2-y2=1,化简得:
(4-k2)x2-2kx-2=0,
记P(x1,y1),Q(x2,y2),
则
|
∴k2<8
| BP |
| BQ |
| 2(1+k2) |
| k2-4 |
令
| BP |
| BQ |
| 4m+2 |
| m-2 |
∵0≤k2≤8
∴0≤
| 4m+2 |
| m-2 |
解得m≤-
| 1 |
| 2 |
| 9 |
| 2 |
故所求
| BP |
| BQ |
| 1 |
| 2 |
| 9 |
| 2 |
| 9 |
| 2 |
点评:本题考查直线和圆锥曲线的位置关系,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
相关题目

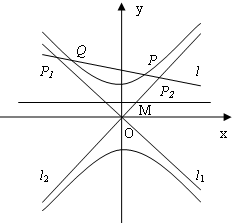 如图,已知双曲线C:
如图,已知双曲线C: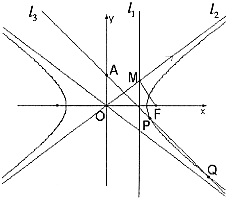 如图,已知双曲线C:
如图,已知双曲线C: 的左、右焦点分别为
的左、右焦点分别为 ,
, ,若λ+μ=4,求双曲线E的方程.
,若λ+μ=4,求双曲线E的方程. 的取值范围.
的取值范围.