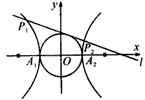
题目内容
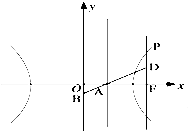 如图,已知双曲线
如图,已知双曲线| x2 |
| a2 |
| y2 |
| b2 |
| OD |
| OF |
| OP |
| AB |
| AD |
(1)求双曲线的离心率;
(2)若a=2,过点B的直线l交双曲线于 M、N两点,问在y轴上是否存在定点C,使?
| CM |
| CN |
分析:(1)先根据条求出A,B,P三点的坐标,结合2
=
+
求出D的坐标,再根据
=λ
(λ≠0)即可求出a和b之间的关系,进而求出曲线的离心率;
(2)先假设存在定点C(0,n)使C
•C
为常数u,设MN的方程为y=kx-1;联立直线方程与双曲线方程求出M,N的坐标与k之间的关系以及k所满足的范围;再求出
•
的值结合
•
为常数即可得出结论.
| OD |
| OF |
| OP |
| AB |
| AD |
(2)先假设存在定点C(0,n)使C
| M |
| N |
| CM |
| CN |
| CM |
| CN |
解答:解:(1)由题得B(0,-b),A(
,0)易得P(c,
),P(c,
)
∵2O
=O
+O
∴D为线段FP的中点 (1分)
∴D(c,
),又A
=λA
,
∵
=λ
(λ≠0)
即A、B、D共线(2分)
∴而A
=(-
,-b),A
=(c-
,
)?,
?∴-
•
-(-b)•(c-
)=0得a=2b
∴e=
=
)2=
=
(4分)?
(2)∵a=2而e=
∴b2=1
∴双曲线方程为
-y2=1①(5分)
∴B(0,-1)
假设存在定点C(0,n)使C
•C
为常数u,设MN的方程为y=kx-1 ②(6分)
由②代入①得(1-4k2)x2+8kx-8=0
由题意得
得k2<
且k2≠
设M(x1,y1),N(x2,y2),
∴x1+x2=
,x1x2=
?(8分)
而C
•C
=(x1,y1-n)•(x2,y2-n)=x1x2+y1y2-n(y1+y2)+n2?
=(1+k2)x1x2-k(n+1)(x1+x2)+(n+1)2=
-
+(n+1)2=u?
整理得:[4(n+1)2-8n-4u]k2+[8-(n+1)2+u]=0 (10分)
对满足k2?
且k2≠
的k恒成立,
∴
解得n=4,u=17
故存在y轴上的定点C(0,4),使C
•C
为常数17 (14分)
| a2 |
| c |
| b2 |
| a |
| b 2 |
| a |
∵2O
| D |
| F |
| P |
∴D为线段FP的中点 (1分)
∴D(c,
| b2 |
| 2a |
| B |
| D |
∵
| AB |
| AD |
即A、B、D共线(2分)
∴而A
| B |
| a2 |
| c |
| D |
| a2 |
| c |
| b2 |
| 2a |
?∴-
| a2 |
| c |
| b2 |
| 2a |
| a2 |
| c |
∴e=
| c |
| a |
1+(
|
1+
|
| ||
| 2 |
(2)∵a=2而e=
| ||
| 2 |
∴双曲线方程为
| x2 |
| 4 |
∴B(0,-1)
假设存在定点C(0,n)使C
| M |
| N |
由②代入①得(1-4k2)x2+8kx-8=0
由题意得
|
| 1 |
| 2 |
| 1 |
| 4 |
设M(x1,y1),N(x2,y2),
∴x1+x2=
| 8k |
| 4k2-1 |
| 8 |
| 4k2-1 |
而C
| M |
| N |
=(1+k2)x1x2-k(n+1)(x1+x2)+(n+1)2=
| 8(1+k2) |
| 4k2-1 |
| 8k2(n+1) |
| 4k2-1 |
整理得:[4(n+1)2-8n-4u]k2+[8-(n+1)2+u]=0 (10分)
对满足k2?
| 1 |
| 2 |
| 1 |
| 4 |
∴
|
故存在y轴上的定点C(0,4),使C
| M |
| N |
点评:本题考查圆锥曲线的性质和应用,解题时要注意公式的灵活运用,认真审题,仔细解答.其中问题(2)是一个开放性问题,考查了同学们观察、推理以及创造性地分析问题、解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
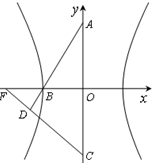 如图,已知双曲线x2-
如图,已知双曲线x2-| y2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 (2013•上海)如图,已知双曲线C1:
(2013•上海)如图,已知双曲线C1: ,曲线C2:|y|=|x|+1,P是平面内一点,若存在过点P的直线与C1,C2都有公共点,则称P为“C1﹣C2型点“
,曲线C2:|y|=|x|+1,P是平面内一点,若存在过点P的直线与C1,C2都有公共点,则称P为“C1﹣C2型点“
 内的点都不是“C1﹣C2型点”
内的点都不是“C1﹣C2型点”