题目内容
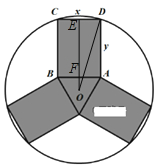
【题目】已知某工厂要设计一个部件(如图阴影部分所示),要求从圆形铁片上进行裁剪,部件由三个全等的矩形和一个等边三角形构成,设矩形的两边长分别为![]() ,
,![]() (单位:cm),且要求
(单位:cm),且要求![]() ,部件的面积是
,部件的面积是![]() .
.

(1)求y关于x的函数表达式,并求定义域;
(2)为了节省材料,请问x取何值时,所用到的圆形铁片面积最小,并求出最小值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 时,面积最小,
时,面积最小,![]() .
.
【解析】
(1)利用已知条件求出![]() ,然后求解函数的定义域即可.
,然后求解函数的定义域即可.
(2)设圆形铁片半径为R,则面积S=πR2,过圆心O作CD的垂线,垂足为E,交AB于点F,连结OD,求出R的表达式,然后利用基本不等式求解最小值即可.
(1)由题意,利用矩形面积和正三角形的面积公式,
可得![]() ,整理得
,整理得![]() ,
,
又由![]() ,解得
,解得![]() ,即函数的定义域为
,即函数的定义域为![]() ,
,
即![]() ,
,![]() .
.
(2)设圆形铁片半径为R,则面积S=πR2,
过圆心O作CD的垂线,垂足为E,交AB于点F,连结OD,则![]() ,
,
所以![]() =
=![]() ,
,
因为x2>0,由基本不等式,可得![]() ,
,
当且仅当![]() ,即
,即![]() 时,取等号,
时,取等号,
所以圆形铁片的最小面积为![]() (cm2),
(cm2),
答:当x=2时,所用圆形贴片的面积最小,最小面积为![]() (cm2).
(cm2).

练习册系列答案
相关题目