题目内容
11.已知数列{an}满足a3=33,an=2an-1+2n-1(n≥2).(1)求a1,a2;
(2)证明:数列{$\frac{{a}_{n}-1}{{2}^{n}}$}为等差数列,并求数列{an}的通项公式.
分析 (1)依次令n=3和n=2,利用递推思想能求出a1,a2.
(2)由已知得${a}_{n}-1=2({a}_{n-1}-1)+{2}^{n}$,n≥2,由此能证明数列{$\frac{{a}_{n}-1}{{2}^{n}}$}为首项是2,公差为1的等差数列,从而能求出数列{an}的通项公式.
解答 (1)解:∵数列{an}满足a3=33,an=2an-1+2n-1(n≥2),
∴33=2a2+23-1,解得a2=13.
13=2a1+22-1,解得a1=5.
(2)证明:∵an=2an-1+2n-1(n≥2),
∴${a}_{n}-1=2({a}_{n-1}-1)+{2}^{n}$,n≥2
∴$\frac{{a}_{n}-1}{{2}^{n}}-\frac{{a}_{n-1}-1}{{2}^{n-1}}$=1,n≥2
∵$\frac{{a}_{1}-1}{2}$=$\frac{5-1}{2}$=2,
∴数列{$\frac{{a}_{n}-1}{{2}^{n}}$}为首项是2,公差为1的等差数列.
∴$\frac{{a}_{n}-1}{{2}^{n}}$=2+(n-1)×1=n+1,
∴${a}_{n}-1=(n+1)•{2}^{n}$,
∴${a}_{n}=(n+1)•{2}^{n}+1$.
点评 本题考查数列的前两项的求法,考查等差数列的证明,考查数列的通项公式的求法,解题时要认真审题,注意构造法的合理运用.

练习册系列答案
相关题目
2.如果y是x的函数,x=$\sqrt{t+1}$,y=$\sqrt{t-1}$,其中t>1,则y与x的函数表达式为( )
| A. | y=$\sqrt{{x}^{2}-2}$ (x>2) | B. | y=$\sqrt{x-2}$(x>2) | C. | y=$\sqrt{{x}^{2}-2}$ (x>$\sqrt{2}$) | D. | y=$\sqrt{x-2}$(x>$\sqrt{2}$) |
19.下列说法正确的个数是( )
①总体个数较少,抽取样本较少时宜采用简单的随即抽样;
②总体各层次差异较大时宜采用分层抽样;
③某工厂在其生产流水线上每隔10取一件产品检验,这种抽样方法叫分层抽样.
①总体个数较少,抽取样本较少时宜采用简单的随即抽样;
②总体各层次差异较大时宜采用分层抽样;
③某工厂在其生产流水线上每隔10取一件产品检验,这种抽样方法叫分层抽样.
| A. | 1 | B. | 2 | C. | 3 | D. | 0 |
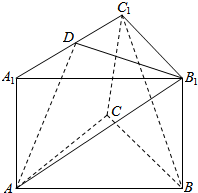 如图,三棱柱ABC-A1B1C1的底面是边长为a的正三角形,侧棱长为$\frac{\sqrt{2}}{2}$a,点D在棱A1C1上.
如图,三棱柱ABC-A1B1C1的底面是边长为a的正三角形,侧棱长为$\frac{\sqrt{2}}{2}$a,点D在棱A1C1上.