题目内容
如图:已知正方体ABCD-A1B1C1D1中,E为棱CC1的中点.如果一只蜜蜂在正方体ABC-A1B1C1D1内部任意飞,则它飞入三棱锥A1-BDE内部的概率为( )


A. | B. | C. | D. |
A
由已知中正方体ABCD-A1B1C1D1中,E为棱CC1的中点.如果一只蜜蜂在正方体ABC-A1B1C1D1内部任意飞,我们设正方体ABCD-A1B1C1D1的棱长为2,分别计算出正方体的体积及棱锥的体积,代入几何概型概率公式,即可得到答案.
解:设正方体ABCD-A1B1C1D1的棱长为2,则
V正方体=8
又∵E为棱CC1的中点,
则BD=A1B=A1D=2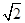 ,BE=DE=
,BE=DE=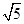 ,A1E=3,
,A1E=3,
设AC与BD交于点O,连接A10,EO,则EO=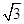 ,A1O=
,A1O=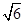
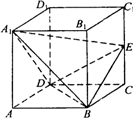
由勾股定理,易得EO⊥A1O,又∵A1O⊥BD,EO∩BD=O
∴A1O⊥平面BDE,即A1O为三棱锥A1-BDE高
∴VA1-BDE=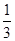 ?SBDE?A1O=2
?SBDE?A1O=2
则它飞入三棱锥A1-BDE内部的概率P=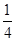
故选A
解:设正方体ABCD-A1B1C1D1的棱长为2,则
V正方体=8
又∵E为棱CC1的中点,
则BD=A1B=A1D=2
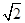 ,BE=DE=
,BE=DE=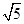 ,A1E=3,
,A1E=3,设AC与BD交于点O,连接A10,EO,则EO=
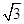 ,A1O=
,A1O=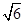

由勾股定理,易得EO⊥A1O,又∵A1O⊥BD,EO∩BD=O
∴A1O⊥平面BDE,即A1O为三棱锥A1-BDE高
∴VA1-BDE=
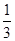 ?SBDE?A1O=2
?SBDE?A1O=2则它飞入三棱锥A1-BDE内部的概率P=
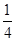
故选A

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
. 个,求
个,求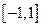 上随机取一个数
上随机取一个数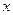 ,使
,使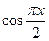 的值介于
的值介于 到1之间的概率为( )
到1之间的概率为( )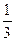

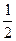
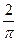
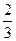
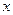 ,第二次出现的点数为
,第二次出现的点数为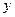 .
.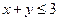 ”
” 的概率;
的概率;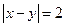 ”的概率.
”的概率. 的分布列为
的分布列为 ,
, ,其中
,其中 为常数,则
为常数,则
 的概率。
的概率。 .
.