题目内容
16.已知等差数列{an}的前n项和Sn,若S2=4,S4=12,则S8等于( )| A. | 36 | B. | 40 | C. | 48 | D. | 24 |
分析 由等差数列的性质可得S2,S4-S2,S6-S4,S8-S6成等差数列,代入已知数据计算可得.
解答 解:由等差数列的性质可得S2,S4-S2,S6-S4,S8-S6成等差数列,
∵S2=4,S4=12,∴4,8,S6-12,S8-S6成等差数列,
∴S6-12=12,S8-S6=16,解得S6=24,S8=40,
故选:B
点评 本题考查等差数列的性质,得出S2,S4-S2,S6-S4,S8-S6成等差数列是解决问题的关键,属基础题.

练习册系列答案
相关题目
11.设不等式组$\left\{\begin{array}{l}{x+y≤2}\\{x≥0}\\{y≥0}\end{array}\right.$表示的平面区域为M,在圆x2+y2=4内随机取一点P,则点P落在M内的概率为( )
| A. | $\frac{1}{4π}$ | B. | $\frac{1}{2π}$ | C. | $\frac{1}{π}$ | D. | $\frac{1}{4}$ |
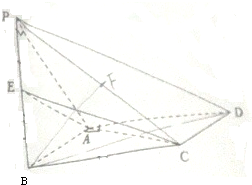 如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,PA⊥PB,BP=BC,E为PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,PA⊥PB,BP=BC,E为PB的中点.