题目内容
7.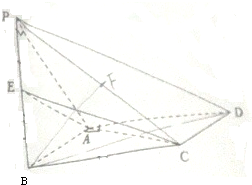 如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,PA⊥PB,BP=BC,E为PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,PA⊥PB,BP=BC,E为PB的中点.(1)求证:PD∥平面ACE;
(2)求证:PA⊥CE;
(3)在线段PC上是否存在一点F,使得BF⊥平面PAC?请说明理由.
分析 (1)首先利用三角形的中位线得到线线平行,进一步转化成线面平行.
(2)首先利用面面垂直转化成线面垂直,进一步转化成线线垂直.
(3)假设存在点F,进一步利用相关的条件得到线线垂直,再转化成线面垂直,从而说明点的存在.
解答 解:(1)在四棱锥P-ABCD中,底面ABCD为矩形,
连接AC,BD交于点O,
∴O为BD的中点,
又∵E为PB的中点.
∴OE∥PD,
∵OE?平面ACE,
PD?平面ACE
∴PD∥平面ACE;
∵平面PAB⊥平面ABCD,
BC⊥AB,
∴BC⊥平面PAB,
∴BC⊥PA.
PA⊥PB,
∴PA⊥平面PBC,
CE?平面PBC,
∴PA⊥CE.
(3)取PC的中点F,
连接BF,由于BP=BC,
∴PBC为等腰三角形.
∴BF⊥PC.
由(2)得:PA⊥平面PBC,
∴PA⊥BF,
∴BF⊥平面PAC.
在线段PC上存在一点F,使得BF⊥平面PAC
点评 本题考查的知识要点:线面平行的判定定理,线面垂直的性质和判定的应用.存在性问题的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.已知等差数列{an}的前n项和Sn,若S2=4,S4=12,则S8等于( )
| A. | 36 | B. | 40 | C. | 48 | D. | 24 |