题目内容
1.在△ABC中,已知b=6$\sqrt{3}$,c=6,C=30°,求a.分析 首先根据正弦定理得出sinB的值进而根据特殊角的三角函数值求出B的值,从而求得角A,再根据正弦定理求出a的值.
解答 解:∵b=6$\sqrt{3}$,c=6,C=30°,
∴由正弦定理可得:sinB=$\frac{bsinC}{c}$=$\frac{6\sqrt{3}×sin30°}{6}$=$\frac{\sqrt{3}}{2}$,
∵0<B<180°,
∴B=60°或120°,
∴A=180°-B-C=90°或30°,
∴a=$\frac{csinA}{sinC}$=12或6$\sqrt{3}$.
点评 本题考查了正弦定理以及特殊角的三角函数值的应用,解题的关键是求出角B的值,属于基本知识的考查.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
16.已知等差数列{an}的前n项和Sn,若S2=4,S4=12,则S8等于( )
| A. | 36 | B. | 40 | C. | 48 | D. | 24 |
11.某研究机构对儿童记忆能力x和识图能力y进行统计分析,得到如下数据:
由表中数据,求得线性回归方程为$\widehaty=\frac{4}{5}$$x+\widehata$,若某儿童的记忆能力为12时,则他的识图能力为( )
| 记忆能力x | 4 | 6 | 8 | 10 |
| 识图能力y | 3 | 5 | 6 | 8 |
| A. | 9.2 | B. | 9.5 | C. | 9.8 | D. | 10 |
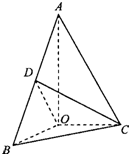 如图,在△AOB中,∠AOB=$\frac{π}{2}$,∠BAO=$\frac{π}{6}$,AB=4,D为线段BA的中点.△AOC由△AOB绕直线AO旋转而成,记∠BOC=θ,θ∈(0,$\frac{π}{2}$].
如图,在△AOB中,∠AOB=$\frac{π}{2}$,∠BAO=$\frac{π}{6}$,AB=4,D为线段BA的中点.△AOC由△AOB绕直线AO旋转而成,记∠BOC=θ,θ∈(0,$\frac{π}{2}$].